Inför tentamen

Tentamensskrivningen kommer att bestå av 5 uppgifter. Skrivningstiden är 4 timmar. Varje uppgift kan ge 6 poäng utom en som kan ge 8 poäng.

Poängsumman från examinationen (tentamen, inlämningsuppgifter, dugga samt bonus från introduktionskursen) avgör betyget på del A av kursen Envariabelanalys I. Betygsgränserna är 25 för trea, 32 för fyra och 40 för femma.

Vid tentamen finns också möjlighet att höja poängen från den löpande examintationen upp till maximalt 18 poäng. Detta sker genom att man löser korrekt valda uppgifter bland sex, som vardera kan ge tre poäng.

Tentamensskrivningen kommer att bestå av tre problem samt två teoriuppgifter.

Teoriuppgifterna kommer att gälla bevis och definitioner som genomgåtts under kursen. Vid tentamen ska man känna till och kunna använda samtliga satser och definitioner.

Följande satser ska dessutom kunna bevisas:

Inkapslingssatsen (Lemma 1.1 i häftet), räkneregeln 1 för gränsvärden (Sats 2.1 i häftet), derivering av en produkt (del 3 i Sats 4.2 i häftet), Kedjeregeln (Sats 5.2 i häftet), satsen om extremvärden till en kontinuerlig funktion (Sats 6.1 i häftet, beviset av lemma 6.1 ingår inte), Medelvärdessatsen (Sats 6.4 i häftet), satsen om konstanta funktioner (Sats 6.6 i häftet), integerbarhet av kontinuerliga funktioner (Sats 8.1 i häftet), satsen om existens av primitiv funktion (Sats 9.2 i häftet).

Följande begrepp och metoder ur kursen är särskilt viktiga för tillämpningar och vidare studier i matematik (H=Häftet)

• funktion, definitionsmängd och värdemängd (sidan 2)
• (strängt) växande/avtagande funktion (sidan 10)
• konkav uppåt/nedåt (sidan 10)
• exponentialt växande/avtagande funktion (sidan 11)
• jämn/udda funktion (sidan 19)
• inverterbar funktion och dess invers (sidan 20)
• den naturliga logaritmen (sidan 23)
• arcusfunktionerna (sidan 34)
• potensfunktion (sidan 37)
• vågrät och lodrät asymptot (sidan 41)
• (uppåt/nedåt) begränsad mängd av reella tal (H sidan 1)
• minsta övre och största under begränsning till en mängd av reella tal (H sidan 1)
• gränsvärde (H sidorna 1 och 2, boken sidan 64)
• deriverbar funktion och dess derivata (H sidan 5, boken sidan 71)
• kontinuitet i en punkt och kontinuerlig funktion (H sidan 4, boken sidan 95)
• parametriserad kurva i planet (sidan 141)
• momentan hastighet hos sådan kurva (sidan 144)
• tangentlinje till graf i en punkt (sidan 150)
• linearisering med fel och relativt fel (H sidan 5, boken sidan 150)
• lokalt maximum/minimum (sidan 167)
• kritisk punkt och kritiskt värde (sidan 167)
• inflexionspunkt (sidan 170)
• största/minsta värde av en funktion (sidan 181)
• hyperboliska funktioner (sidan 204)
• över- och undersumma (H sid 11)
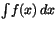• $\int\!f(x)\,dx$ (H sid 11)
• primitiv funktion (antiderivative) (H sidan 12, boken sidan 262)
• partialbråksuppdelning (sidan 312)
• trapetsregeln (sidan 318)
• Simpsons regel (sidan 324)
• konvergens/divergens av generaliserad (improper) integral (sidorna 327 och 331).