- Figuren nedan är (en del av) grafen till ett av
polynomen. Vilket?
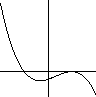
a) -(x+1)(x-1)2 b) (1-x)(x+1)2 c) -x(x2-1) d) -(x2+1)(x-1) e) (x+1)(x-1)3
- En av figurerna nedan illustrerar (en del av) grafen till
f(x)=x2/(1-x4). Vilken?
a) ![\includegraphics [scale=1]{duggaTMA305aH02fig2.eps}](img3.gif)
b) ![\includegraphics [scale=1]{duggaTMA305aH02fig3.eps}](img4.gif)
c) ![\includegraphics [scale=1]{duggaTMA305aH02fig4.eps}](img5.gif)
d) ![\includegraphics [scale=1]{duggaTMA305aH02fig5.eps}](img6.gif)
e) ![\includegraphics [scale=1]{duggaTMA305aH02fig6.eps}](img7.gif)
- En av följande ekvationer är en ekvation för tangentlinjen till
grafen av funktionen
f(x)=x/(1+x2) i punkten där
x=2. Vilken?
a) y=3(x-2)/5+1 b) y=3(x-2)/25+2/5 c) y=3(x-2/5)+2 d) y=2x+3 e) y=3(2-x)/25+2/5
- Följande figur visar (en del av) grafen till f'(x).
[scale=1]duggaTMA305aH02fig7.epsVilken av följande figurer illustrerar (en del av) grafen till f(x).
a) ![\includegraphics [scale=1]{duggaTMA305aH02fig8.eps}](img8.gif)
b) ![\includegraphics [scale=1]{duggaTMA305aH02fig9.eps}](img9.gif)
c) ![\includegraphics [scale=1]{duggaTMA305aH02fig10.eps}](img10.gif)
d) ![\includegraphics [scale=1]{duggaTMA305aH02fig11.eps}](img11.gif)
e) ![\includegraphics [scale=1]{duggaTMA305aH02fig12.eps}](img12.gif)
- Vad är f'(1), när
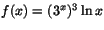 ?
?
a) -3 b) 1 c) 27 d) -9 e)
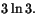
- Om funktionen f(x) vet man att den är konkav uppåt i
intervallet [1,3] och strängt avtagande i [-1,1]. Vilken figur
illustrerar (en del av) grafen till f(x)?
a) ![\includegraphics [scale=1]{duggaTMA305aH02fig13.eps}](img15.gif)
b) ![\includegraphics [scale=1]{duggaTMA305aH02fig14.eps}](img16.gif)
c) ![\includegraphics [scale=1]{duggaTMA305aH02fig15.eps}](img17.gif)
d) ![\includegraphics [scale=1]{duggaTMA305aH02fig16.eps}](img18.gif)
e) ![\includegraphics [scale=1]{duggaTMA305aH02fig17.eps}](img19.gif)
- Nedan illustrerar graferna till f(x) respektive
f(g(x)). Med ledning av dessa, vad är g'(1)?
![\includegraphics [scale=1]{duggaTMA305aH02fig18.eps}](img20.gif)
![\includegraphics [scale=1]{duggaTMA305aH02fig19.eps}](img21.gif)
a) -1 b) 3 c) -2 d) -1/4 e) 1/4
- Vad är gränsvärdet av
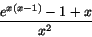
när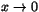 ?
?
a) 1/2 b) 3 c) -3/2 d) 3/2 e) -2/3
- Det finns bara ett värde på a så att
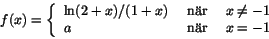
blir deriverbar i -1. Vad är då f'(-1)?a) -1/2 b) 1/2 c) 3 d) -1/3 e) 0
- Det finns bara ett värde på a så att
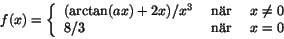
blir kontinuerlig i 0. Vilket är detta värde på a?a) 1/3 b) -2 c) 8/5 d) 8/3 e) 8
- En parametriserad kurva i planet ges av
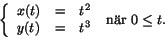
En av följande ekvationer är en ekvation för tangetlinjen till kurvan när t=1. Vilken?
a) y=3(x-1)/2+1 b) y=3(x-2)/2+1 c) y=5(1-x)+1 d) y=7(x-2)/3+2 e) y=(x-3)+1
- Hur många lösningar har ekvationen
2x+3-x=7x/2?
a) 3 b) 1 c) inga d) 2 e) -1
Jan-Alve Svensson
2002-09-27