- Figuren nedan är (en del av) grafen till en av funktionerna i
alternativen. Vilket alternativ stämmer?
![\includegraphics [scale=1]{figA1.eps}](img3.gif)
a) f(x)=2x2/(x-1)2 b) f(x)=2x2/(x2-1) c) f(x)=x/(x-1)2
d) f(x)=-x/(x-1)2 e)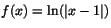 .
.
- Figuren nedan illustrerar (en del av) grafen till en av funktionerna i alternativen. Vilket alternativ stämmer?
![\includegraphics [scale=1]{figB1.eps}](img5.gif)
a) f(x)=4-e1-x b)
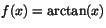 c)
c) 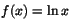
d) f(x)=(x+1)2/(x2+1) e) f(x)=4-ex-1. - Ett av alternativen illustrerar (en del av) grafen till
f(x)=1+x-x2-x3. Vilket?
a) ![\includegraphics [scale=1]{figD4.eps}](img8.gif)
b) ![\includegraphics [scale=1]{figD1.eps}](img9.gif)
c) ![\includegraphics [scale=1]{figD2.eps}](img10.gif)
d) ![\includegraphics [scale=1]{figD5.eps}](img11.gif)
e) ![\includegraphics [scale=1]{figD3.eps}](img12.gif)
- En av alternativen ger det korrekta värdet av
 . Vilket?
. Vilket?
a) 3 b)
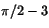 c)
c) 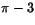 d)
d) 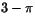 e)
e) 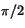 .
.
- Ett av följande alternativ är ett korrekt påstående. Vilket?
a)
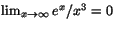 b)
b)
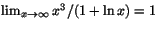
c)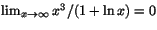 d)
d)
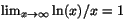
e)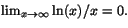
- Ett av alternativen anger en funktion som har den linjära
approximationen 3x-5 i närheten av 2. Vilket?
a)
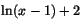 b)
(x2+4x-3)/(x4-2x3+9)
b)
(x2+4x-3)/(x4-2x3+9)
c) (x2+3x-8)/(x3-11x+16) d) ex2-x+1 e) x2-x+1. - Ett av alternativen nedan anger en funktion som är strängt
växande och konkav uppåt ibland och konkav nedåt ibland. Vilket?
a) f(x)=ex3-x+1 b)
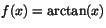 c)
f(x)=x2+3x+1
c)
f(x)=x2+3x+1
d)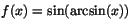 e)
e)
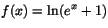 .
.
- Ett av alternativen nedan anger en funktion f(x) med derivata
f'(x)=2x/(1+x2). Vilket?
a)
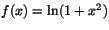 b)
b)
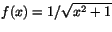 c)
c)
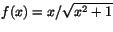
d) f(x)=(2x3+2x-4x2)/(1+x2)2 e) f(x)=x2/(x+(x3/3)). - Graferna nedan illustrerar delar av graferna till funktionen
f(x) respektive g(x). Vilket av alternativen illustrerar bäst
derivatan till f(g(x))?
![\includegraphics [scale=1]{figC1.eps}](img29.gif)
![\includegraphics [scale=1]{figC2.eps}](img30.gif)
a) ![\includegraphics [scale=1]{figC4.eps}](img31.gif)
b) ![\includegraphics [scale=1]{figC5.eps}](img32.gif)
c) ![\includegraphics [scale=1]{figC6.eps}](img33.gif)
d) ![\includegraphics [scale=1]{figC7.eps}](img34.gif)
e) ![\includegraphics [scale=1]{figC3.eps}](img35.gif)
- Ett av följande påståenden är korrekt. Vilket?
a) Om f(x) och g(x) är strängt växande, så är f(x)g(x) strängt växande.
b) Om f(x) är strängt växande, så är f-1(x) strängt avtagande.
c) Om f(x) är strängt växande och konkav nedåt, så finns det en konstant K, så att f(x)<K, för alla x.
d) Om f(x) är strängt växande och konkav nedåt, så är f-1(x) konkav uppåt.
e) Om f(x) är strängt växande och f'(x) är strängt avtagande, så finns det en konstant K, så att f(x)<K, för alla x. - Går det att bestämma konstanten a så att funktionen
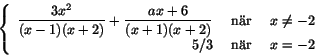
blir kontinuerlig i x=-2?
a) Nej b) Ja, a=5 c) Ja, a=3 d) Ja, a=-5 e) Ja,
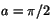 .
.
- Går det att bestämma konstanten a, så att funktionen
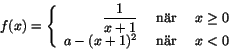
blir deriverbar i x=0?a) Nej b) Ja, a=5 c) Ja, a=3 d) Ja, a=-5 e) Ja, a=2.