- Grafen har (förefaller ha) en vågrät asymptot. Detta utesluter
aleternativ c) - d). Den har en lodrät asymptot detta
utesluter b).
Rätt alternativ: a)
- Alternativ b) och c) är uteslutna på grund av funktionens värde
i x=0. I alternativ e) går funktionen mot
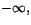 när
när
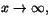 vilket utesluter detta alternariv.
vilket utesluter detta alternariv.
I alternativ d) ger en omskrivning att f(x)=1+(2x)/(1+x2), med derivata f'(x)=(2-4x2)/(x2+1)2, som växlar tecken i 1/2. Detta stämmer inte med figuren.
Rätt alternativ: a)
- Man har att
f(x)=1+x-x2-x3=(1+x)(1-x2), som har
nollställen i -1 (dubbelt) och 1. Detta utesluter a) och
d). Vidare gäller att
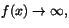 när
när
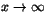 , vilket utesluter c).
, vilket utesluter c).
Eftersom f(0)=1 är e) uteslutet.
Rätt alternativ: b)
- Man har att
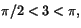 så
så 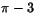 är en vinkel mellan 0 och
är en vinkel mellan 0 och
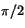 med samma sinus-värde som 3. Detta ger att
med samma sinus-värde som 3. Detta ger att
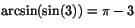 .
.
Rätt alternativ: c)
- Man har att en expontentiellt växande funktion dominerar en
potensfunktio, och att en växande potensfunktion dominerar
logaritmer när
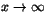 .
.
I a), b) och c) går uttrycket mot
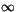 . I d) och e) går det mot
0.
. I d) och e) går det mot
0.
Rätt alternativ: e)
- Att 3x-5 är den linjära approximationen till f(x) i x=2,
ger att
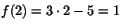 och f'(2)=3.
och f'(2)=3.
Värdet 1 när x=2 utesluter d) och e) . I a) är derivatan 1/(x-1), som ger 1 när x=2, vilket utesluter detta alternativ.
I b) är derivatan ((2x+4)(x4-2x3+9)-(x2+4x-3)(4x3-8x))/(x4-2x3+9), som blir
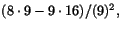 som är negativt (alltså inte
3).
som är negativt (alltså inte
3).
I c) är derivatan ((2x+3)(x3-11x+16)-(x2+3x-8)(3x2-11))/(x3-11x)+16)2 som blir
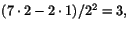 som stämmer.
som stämmer.
Rätt alternativ: c)
a) Derivatan är (3x2-1)ex3-x+1, som växlar tecken. Funktionen är inte strängt växande.
b) Derivatan är 1/(1+x2), som alltid är positivt. Funktionen är strängt växande. Andra derivatan är -2x/(1+x2)2, som växlar tecken. Funktionen växlar konkavitet.
c) Derivatan är 2x+3 som växlar tecken. Funktionen är inte strängt växande.
d) Funktionen är f(x)=x som inte växlar konkavitet.
e) Derivatan är ex/(ex+1)=1-(1/(ex-1)) som alltid är positivt. Funktionen strängt växande. Andraderivatan är ex/(ex-1)2, som inte växlar tecken (är positiv). Funktionen byter inte konkavitet.
Rätt alternativ: b)
- I a) är derivatan
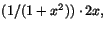 som är det sökta.
som är det sökta.
Rätt alternativ: a)
- Kedjeregen ger
D(f(g(x)))=f'(g(x))g'(x), som är =0 när
antingen g'(x)=0 (som stämmer för två värden på x, i närheten av
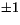 ) eller f'(g(x))=0. Den sista likheten ger g(x)=0 som
har lösningen x=0.
) eller f'(g(x))=0. Den sista likheten ger g(x)=0 som
har lösningen x=0.
Den graf som gäller ska alltstå ha precis tre nollställen.
Rätt alternativ: e)
- a) Stämmer inte: tag f(x)=g(x)=x.
b) Stämmer inte: tag f(x)=ex med invers
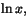 som båda är strängt växande.
som båda är strängt växande.
c) Stämmer inte: tag
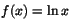 som är strängtväxande, konkav nedåt
men
som är strängtväxande, konkav nedåt
men
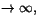 när
när
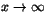 .
.
d) Om f(x) är konkav nedåt ligger grafen under varje tangentlinje. Speglas bilden i linjen x=y hamnar grafen (till f-1(x)) ovanför tangetlinjen i varje punkt. (Att f(x) är strängtväxande gör att man kan vara säker på att den är inverterbar.)
e) Stämmer inte: tag
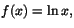 med f'(x)=1/x som är positiv (när
x>0, så att f(x) växer) men strängt avtagande. Dessutom
f(x)
med f'(x)=1/x som är positiv (när
x>0, så att f(x) växer) men strängt avtagande. Dessutom
f(x)
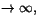 när
när
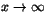 .
.
Rätt alternativ: d)
- Uttrycket för f(x) när
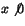 skrivs på ett bråkstreck:
skrivs på ett bråkstreck:
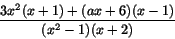
För kontinuitet i x=-2 krävs att detta uttryck har gränsvärdet 5/3 när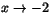 . Eftersom nämnaren blir 0 när x=-2 måste
även täljaren bli det. Detta ger
-12+(-2a+6)(-3)=0 eller a=5.
. Eftersom nämnaren blir 0 när x=-2 måste
även täljaren bli det. Detta ger
-12+(-2a+6)(-3)=0 eller a=5.
Detta ger bråket
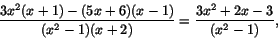
som har gränsvärdet (12-4-3)/3=5/3.Rätt alternativ: b)
För deriverbarhet krävs kontinuitet. Man ska ha 1/(0+1)=a-(0+1)2 som ger a=2. För deriverbarhet krävs dessutom att derivatorna av 1/(x+1) och 2-(x+1)2 blir samma när x=0.
Det första uttrycket har derivatan -1/(x+1)2, som ger -1, när x=0. Det andra har derivatan -2(x+1) som blir -2, när x=0.
Rätt alternativ: a)