Lösning av TMA305 Envariabelanalys I, del a, 02 10 21

 
1. Fyrhörningen med hörn i origo, (0,1), P och (2,0) har arean

ab+a(1-b)/2+(2-a)b/2=a/2+b.

Eftersom triangeln med hörn i origo, (0,1) och (2,0) har arean $2\cdot 1/2=1$ ger detta att triangeln med hörn i (0,1), P och (2,0) har arean a/2+b-1. Eftersom (a,b) ligger på ellipsen har vi att a²/4+b²=1, så $a/2=\pm\sqrt{1-b^{2}},$ där bara plustecknet är aktuellt. Detta ger

$$A(b)=\sqrt{1-b^{2}}+b-1,$$

där A(b) är triangelns area när P har y-koordinaten b. Vi söker b så att A(b) är störst möjlig. Ett sådant värde på b är en kritisk punkt till A(b), vilket ger oss

$$0=A'(b)=-b/\sqrt{1-b^{2}}+1=(\sqrt{1-b^{2}}-b)/\sqrt{1-b^{2}}).$$

Vi får $b=\sqrt{1-b^{2}},$ som efter kvadrering blir 2b²=1, eller $b=\pm 1/\sqrt{2},$ där bara plustecknet är giltigt. Detta ger $a=2\sqrt{1-1/2}= \sqrt{2}$.
 
Svar: $P=(\sqrt{2},1/\sqrt{2})$.
 
2. Av formeln för funktionen ser vi att den är deriverbar utom möjligen i x=0. Differenskvoten där är

$$Q=\frac{\ln(ax+1)-2x-bx^{2}}{x^{3}},$$

som ger ett gränsvärde av typ ``0/0'', när $x\rightarrow 0$. l'Hospitals regel ger oss kvoten

$$Q_{1}=\frac{a/(ax+1)-2-2bx}{3x^{2}},$$

där nämnaren går mot noll när $x\rightarrow 0$. För att gränsvärdet ska finnas måste då också täljaren gå mot noll. Detta ger 0=a-2, dvs a=2. Detta och ytterligare användning av l'Hosptials regel ger

$$Q_{2}=\frac{-4/(2x+1)^{-2}-2b}{6x}$$

Av samma skäl som tidigare måste täljaren gå mot noll: 0=-4-2b, eller b=-2. Ytterligare användning av l'Hospitals regel ger

$$Q_{3}=\frac{16/(2x+1)^{-3}}{6},$$

som har gränsvärdet 16/6=8/3, när $x\rightarrow 0$. Enligt l'Hospitals sats har Q samma gränsvärde och vi får f'(0)=8/3. Eftersom a=2 är funktionen definierad när 2x+1>0, eller när x>-1/2, på grund av logaritmfunktionens förekomst. Funktionen har derivatan

$$f'(x)=\left\{ \begin{array}{lcr} -2x^{-3}\ln(2x+1)+x^{-2... ...r } &x\neq 0\\ 8/3 & \mbox{ när } &x=0 \end{array}\right.$$

som vi ser är kontinuerlig ( när x>-1/2) utom möjligen i x=0. För att undersöka kontinuitet där ska vi undersöka gränsvärdet av

$$f'(x)=Q=\frac{-2(2x+1)\ln(2x+1)+2x+2x(2x+1)}{x^{3}(2x+1)}$$

när $x\rightarrow 0$. Om detta finns och blir f'(0)=8/3, är f'(x) kontinuerlig i x=0, annars inte. Vi ser att detta är ett gränsvärde av typen ``0/0'' och l'Hospitals regel ger kvoten

$$Q_{1}=\frac{-4\ln(2x+1)-4+2+8x+2}{8x^{3}+3x^{2}}$$

som ger gränsvärde av samma typ. Ytterligare användning av regeln ger

$$Q_{2}=\frac{-8(2x+1)^{-1}+8}{24x^{2}+6x}$$

som ger gränsvärde av samma typ igen. Ytterligare användning av regeln ger

$$Q_{3}=\frac{16(2x+1)^{-2}}{48x+6}$$

som har gränsvärdet 16/6=f'(0), när $x\rightarrow 0$. l'Hospitals regel ger att även f'(x) har detta gränsvärde när $x\rightarrow 0$. Därmed är f'(x) kontinuerlig även i x=0.
 
Svar: a=2, b=-2, funktionen är definierad när x>-1/2 och derivatan är kontinuerlig.
 
3.
 

(a) Vi har med hjälp av trigonometriska ettan att

$$I=\int\!\frac{\cos t}{\sqrt{1+\cos^{2}t}}\,dt=\int\!\frac{\cos t}{\sqrt{2-\sin^{2} t}}\,dt$$

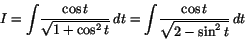
eller

$$I=\frac{1}{\sqrt{2}}\int\!\frac{\cos t}{\sqrt{1-(\sin(t)/\sqrt{2})^{2}}}\,dt,$$

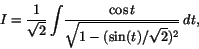
vilket leder oss till variabelsubstitutionen $x=\sin(t)/\sqrt{2}$. Vi får då

$$I=\int\!\frac{1}{\sqrt{1-x^{2}}}\,dx=\arcsin{x}=\arcsin(\sin(t)/\sqrt{2}).$$

 
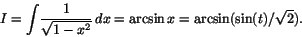
Svar: $\arcsin(\sin(t)/\sqrt{2})$.
 
(b) Faktorisering av nämnaren som har nollstället 1/2, ger

2t³+3t²+2t-2=(2t-1)(t²+2t+2)

där faktorn av grad två saknar reella nollställen. Partialbråksuppdelning ger

$$\frac{5t+4}{2t^{3}+3t^{2}+2t-2}=\frac{2}{2t-1}-\frac{t}{t^{2}+2t+2}.$$

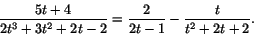
Det första bråket har den primitiva funktionen $F_{1}(t)=\ln(2t-1)$. Det andra bråket skriv om:

$$\frac{t}{t^{2}+2t+2}=\frac{1}{2}\frac{2t+2}{t^{2}+2t+2}-\frac{1}{(t+1)^{2}+1},$$

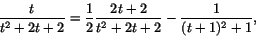
där det första bråket har den primitiva funktionen
$F_{2}(t)=(1/2)\ln(t^{2}+2t+2)$ och det andra $F_{3}(t)=\arctan(t+1)$. Den ursprungliga rationella funktionen har därför den primitiva funktionen

F(t)=F₁(t)-F₂(t)+F₃(t),

eller

$$F(t)=\ln((2t-1)/\sqrt{t^{2}+2t+2})+\arctan(t+1).$$

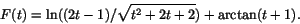
Eftersom $F(t)\rightarrow \ln(2)+\pi/2,$ när $t\rightarrow \infty$ och $F(2)=\ln(3/\sqrt{10})+\arctan(3),$ blir integralen i uppgiften konvergent med värdet $\ln(2\sqrt{10}/3)+\pi/2-\arctan(3)$.
 
Svar: Integralen är konvergent med värdet
$(1/2)\ln(40/9)+\pi/2-\arctan(3)$.
 

6. Man har $f'(x)=2^{x}+x2^{x}\ln 2,$ så $f'(1)=2^{1}+1\cdot 2\ln 2=2(1+\ln 2)$.
 
Svar: $2(1+\ln 2)$.
 
7. Enligt kedjeregeln är (f(g(x)))'=f'(g(x))g'(x). Derivatan av den sammansatta funktionen är därför, när x=1, f'(g(1))g'(1)=f'(2)9=(1/3)9=3.
 
Svar: 3.
 
8. Partiell integration ger

$$\int\!(t^{2}+1)e^{t}\, dt=(t^{2}+1)e^{t}-\int\!2te^{t}\,dt=$$

$$=(t^{2}+1)e^{t}-2te^{t}+\int\!2e^{t}\,dt=(t^{2}-2t+3)e^{t}.$$

 
Svar: (t²-2t+3)e^t.
 
9. Tangentlinjen går genom $(x(1),y(1))=(\pi/4,0)$ och har riktningskoefficient y'(1)/x'(1). Vi har x'(t)=1/(1+x²) och y'(t)=1/(2t), så riktningskoefficienten blir (1/2)/(1/2)=1. Tangentlinjens ekvation blir $y=1\cdot(x-\pi/4)+0$.
 
Svar: $y=x-\pi/4$.
 
10. Skrivning på gemensamt bråkstreck ger uttrycket

$$\frac{t+1+a}{(t-1)(t+1)}.$$

Eftersom nämnaren går mot noll när $x\rightarrow 1,$ måste även täljaren göra det om gränsvärdet ska existera. Detta ger 0=1+1+a, så a=-2. Efter förkortning blir uttrycket 1/(t+1), som har gränsvärdet 1/2, när $x\rightarrow 1$.
 
Svar: a=-2 och gränsvärdet blir 1/2.
 
11. Vi skriver om uttrycket som ska integreras:

$$\frac{x}{\sqrt{2+x-x^{2}}}=-\frac{1}{2}\frac{1-2x}{\sqrt{2+x-x^{2}}}+\frac{1}{2}\frac{1}{\sqrt{9/4-(x-1/2)^{2}}},$$

där den första kvoten till höger har den primitiva funktionen $F_{1}(x)=-\sqrt{2+x-x^{2}}$. Den andra kvoten skrivs om:

$$\frac{1}{2}\frac{1}{\sqrt{9/4-(x-1/2)^{2}}}=\frac{1}{3}\frac{1}{\sqrt{1-((2x-1)/3)^{2}}},$$

som har den primitiva funktionen $F_{2}(x)=\arcsin((2x-1)/3)/2$. En primitiv funktion till det ursprungliga uttrycket är därför F(x)=F₁(x)+F₂(x). Vi har $F(x)=F_{1}(x)+F_{2}(x)\rightarrow -0+\arcsin(1)/2=\pi/4,$ när $x\rightarrow 2,$ och $F(1/2)=-\sqrt{9/4}-\arcsin(0)/2=-3/2,$ så integralen blir konvergent med gränsvärdet $\pi/4+3/2$.
 
Svar: Integralen är konvergent med värdet $\pi/4+3/2$.