Lösning av TMA305 Envariabelanalys I, del a, 03 01 13
- Man har
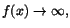 när
när
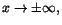 så
f antar säkert ett minsta värde. Detta antas när f'(x)=0. Man har
så
f antar säkert ett minsta värde. Detta antas när f'(x)=0. Man har
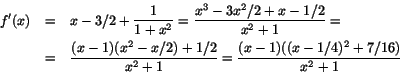
så enda nollstället är x=1 och där är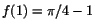 .
.
Svar: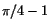 .
.
- Man ska bestämma a så att kvoten
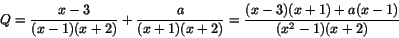
har ett gränsvärde när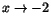 .
Eftersom nämnaren går mot 0 när
.
Eftersom nämnaren går mot 0 när
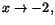 måste även
täljaren göra det för att gränsvärdet ska finnas. Detta ger
a=5/3. Insättning av detta och förkortning med x+2 ger
måste även
täljaren göra det för att gränsvärdet ska finnas. Detta ger
a=5/3. Insättning av detta och förkortning med x+2 ger
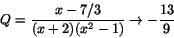
som ska vara b för kontinuitet.
Svar: a=5/3 och b=-13/9. -
(a) Man har
![\begin{eqnarray*}
\int_{3}^{8}\frac{\sqrt{t+1}}{t+\sqrt{t+1}+1}\,dt&=&\left\{x...
...\Big)\, dx=\\
&=&\Big[2x-2\ln(x+1)\Big]_{2}^{3}=2-2\ln(4/3)
\end{eqnarray*}](img10.gif)
Svar: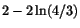
(b) Man har
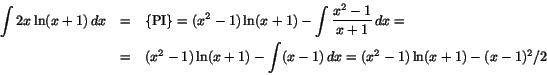
6. Man har
Svar: 1.
7. Man har f-1(1)=2 och (df-1/dx)(1)=1/f'(2)=3.
Svar: 3.
8. Man har
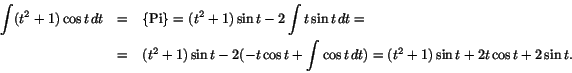
Svar:
9. Man har x'=2t/(1+t4) och y'=2t som ger tangentvektorn (1,2), när t=1. Tangetlinjen har alltså riktingskoefficienten 1/2 och går genom
Svar:
10. Man har
Eftersom nämnaren går mot 0 när
när
11. Man har
![\begin{eqnarray*}
\int_{0}^{1}\frac{x}{\sqrt{1-x^{2}}}\,dx&=&\Big[-\sqrt{1-x^{2}}\Big]_{0}^{1}\\
&=&1
\end{eqnarray*}](img23.gif)
Svar: 1.
Jan-Alve Svensson
2003-01-09