Tentamen i TMA 305 Envariabelanalys I, del A,
01 10 25, kl 8.45-11.45.
- 1.
- Finns det något plan som går genom de fyra punkterna (2,5,3),
(-2,1,2), (3,-1,-2) och (1,2,1)? Motivera svaret noggrant!
- 2.
- Bestäm konstanten a så att funktionen
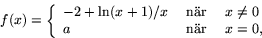
som är definierad för x>-1, blir deriverbar över allt. Är derivatan
kontinuerlig?
- 3.
- Man drar en tangentlinje till funktionen f(x)=e-x i en punkt
(a,f(a)), där a>0. Den skär x- och y-axeln i P respektive
Q och man låter A vara arean av triangeln med hörn i dessa båda
punkter samt origo. Har A ett största eller minsta värde? Vad är
de i så fall?
- 4.
- (a)
- Vad menas med en över- respektive undersumma till en funktion
f som är begränsad på ett intervall [a,b]? (Ge en matematisk definition.)
- (b)
- Hur lyder definitionen av att en funktion f, som är begränsad
på [a,b], är integrerbar? Vad betyder i så fall
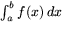 ?
?
- (c)
- Funktionen f(x) definieras som f(x)=2x, när x är ett
rationellt tal och f(x)=1 annars. Existerar
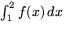 ? Motivera noggrant!
? Motivera noggrant!
- 5.
- Formulera och bevisa medelvärdessatsen.
JAS
![]()
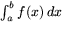 ?
?
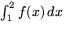 ? Motivera noggrant!
? Motivera noggrant!