Tentamen i TMA 305 Envariabelanalys I, del A, 03 01 13, kl 14.15-18.15.

1. Motivera att funktionen
   
   $$f(x)=\frac{x^{2}}{2}-\frac{3x}{2}+\arctan x$$
   
   
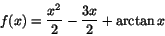
   har ett minsta värde och bestäm detta.

 

2. Undersök om det är möjligt att bestämma konstanterna a och b så att funktionen
   
   $$\begin{eqnarray*} f(x)=\left\{ \begin{array}{lcr} {\displaystyle \frac{x-3... ...& x\neq -2\\ b & \mbox{ när } & x=-2 \end{array} \right. \end{eqnarray*}$$
   
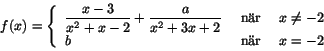
   blir kontinuerlig i x=-2. Motivera noggrant!

 

3. Beräkna (a)
   
   $$\int_{3}^{8}\frac{\sqrt{t+1}}{t+\sqrt{t+1}+1}\,dt$$
   
   
   
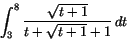
   (b)
   
   $$\int 2x\ln(x+1)\, dx.$$
   
   
   
   

 

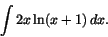
4. (a) Vad är den precisa matematiska innebörden av att f(x) är deriverbar i x=a?
    
   (b) Ge, om möjligt, exempel på en funktion som är kontinuerlig i en omgivning till x=0, men inte deriverbar där?
    
   (c) Ge, om möjligt, exempel på en funktion som är dervierbar i en omgivning till x=0, men derivatan inte är kontinuerlig där?
    
   
5. Visa att om en funktion f(x) är kontinuerlig på intervallet [a,b], så antar den ett största och ett minsta värde där.

 
Under kursens gång har det förekommit löpande examination. Den maximala poängen från denna är 18. Om Du vill komplettera Din poäng från detta moment kan Du lösa uppgifter nedan. Inom parentes vilka uppgifter som är aktuella för Dig. T.ex. anger (< 12) att uppgiften gäller Dig vars poäng från den löpande examinationen är < 12. Bara korrekt valda uppgifter kommer att beaktas! Varje uppgift kan ge tre poäng. Tillsammans med den löpande examinationen kan Du dock högst komma upp i den poäng som anges inom parentes. Det betyder att om Du t.ex. har 11p från tidigare examination och löser uppgift 9 helt korrekt, så kommer Du trots detta bara upp i 12p. Fullständiga lösningar krävs för poäng!
 
   6. (<3) Bestäm f'(1) när $f(x)=x\ln x$.
 
   7. (<6) Man vet att f är inverterbar och att f(2)=1 samtf'(2)=1/3. Beräkna inversens derivata i x=1.
 
   8. (<9) Beräkna $\int (t^{2}+1)\cos t\,dt$.
 
   9. (<12) En parametriserad kurva i planet ges av $x(t)=\arctan(t^{2}),$ y(t)=t²+1, där t>0. Bestäm en ekvation för tangentlinjen till kurvan när t=1.
 
   10. (<15) Bestäm konstanten a så att

$$\frac{a}{t-2}+\frac{2}{t^{2}-4}$$

har ett gränsvärde när $t\rightarrow 2$. Bestäm också gränsvärdet i detta fall.
 
   11. (<18) Beräkna

$$\int_{0}^{1}\frac{x}{\sqrt{1-x^{2}}}\, dx$$

om den konvergerar. Visa annars att den divergerar.
 
JAS