x' = x(1 - y)betyder att bestämma alla prarametriserade kurvor (x(t), y(t)) som satisfierar det. Högra leden ger för punkter (x, y) en vektor (x(1 - y, ;y(x - 1) (vektorfältet). Vänstra leden ger (x(t), y(t)) som är kurvans hastighet. För att lösa ekvationen ska man alltså bestämma kurvor med förutbestämd hastighet i punkter längs kurvan.
y' = y(x - 1)
För att illustrera vektorfältet kan man i ett antal punkter (x, y) avsätta vektorn (x(1 - y), y(x - 1) .
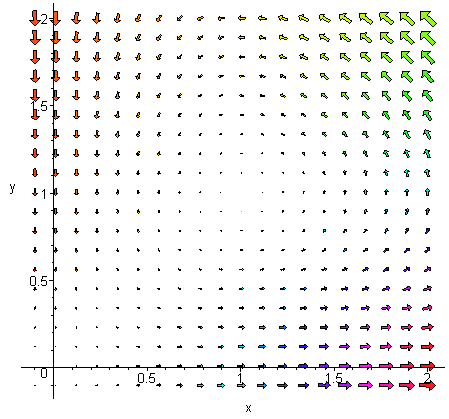
Observera att, för bildens tydlighet, skalan på vektorernas längd inte är samma som skalan längs axlarna.
Ett annat sätt att illustrera ekvationen är att rita enhetsvektorer i vektorfältets riktning (riktningsfältet)
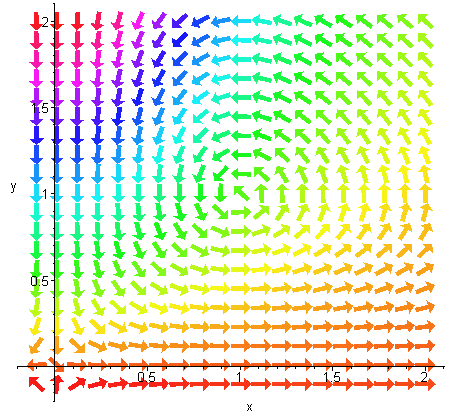
Ett tredje sätt att illustrera ekvationen är att bara rita vektorfältets lutning(riktningsfältet)
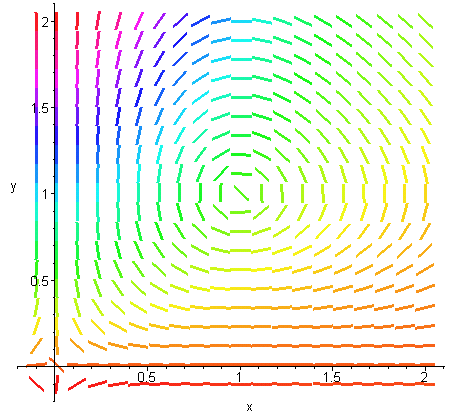
Ett försök att illustrera en lösning till systemet med x(0) = 0.5 och y(0) = 0.7 . Systemet kan inte lösas exakt men programvara ger:
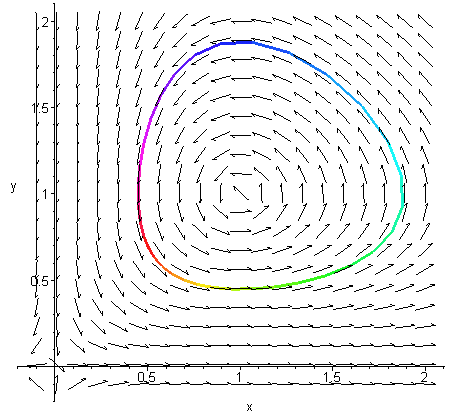
Kurvan byter färg i takt med tiden, från (infra)rött vid t = 0 till (ultra)violett (vid t = 6.5 ).
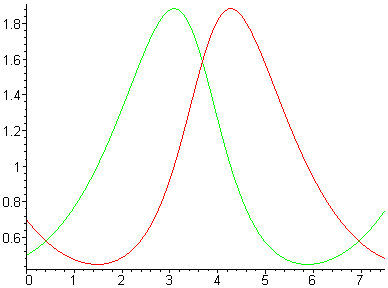
Graferna till x(t) och y(t) ser ut så här (med hjälp av programvara)
Jan Alve Svensson <janalve@math.chalmers.se> Last modified 2002-11-18 at 13:31 by Jan Alve Svensson, janalve@math.chalmers.se