Två lösningar till
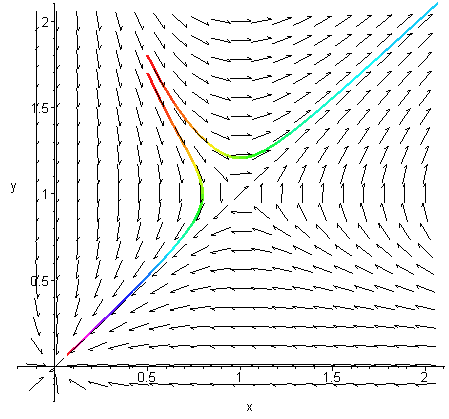
x' = x(y - 1)
y' = y(x - 1)
Om man tolkar x(t) och
y(t) som antalet av två sammexisterade arter
vid tiden t har båda arterna nytta av varandra i
denna model. (Symbios.)
Lösningarna börjar i rött ( t = 0 ) och
övergår i violett i takt med tiden. Observera att två närliggande
startpunkter leder till radikalt olika slutpunkter.
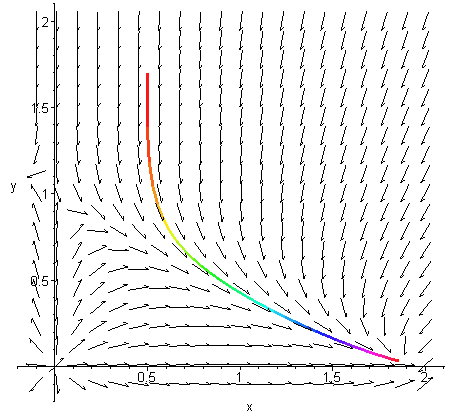
En lösning till
x' = x(1 - x/2 - y/2)
y' = y(1 - x - y)
Om man tolkar x(t) och
y(t) som antalet av två sammexisterade arter
vid tiden t har hämmas båda arterna den andras
existens. (Konkurrens.)
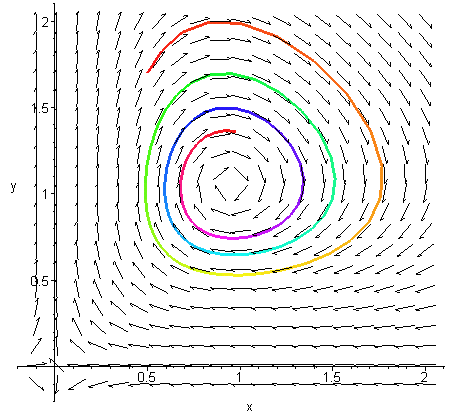
En lösning till
x' = x(y - 1 - 0.05x)
y' = y(1 - x - 0.05y)
Om man tolkar x(t) och
y(t) som antalet av två sammexisterade arter
vid tiden t har gynnas första arten av den andra
medan den andra missgynnas av den första. (Rovdjur/byte.)
Jan Alve
Svensson <janalve@math.chalmers.se>
Last modified 2002-11-18 at 13:31 by
Jan Alve Svensson,
janalve@math.chalmers.se
|