Dugga i TMA 305B Envariabelanalys I, del B,
02 11 23, kl 8.45-10.45.
- Ett plan har normalen (1,2,3) och går genom (1,1,1). Vilken
ekvation har planet?
a) x+2y+3z-3=0 b) x+y+z=6 c) x+2y+3z=6
d) -x+2y-z=0 e) -x+2y-z=3 - Man vet att
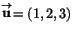 och
och
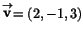 . Vad är då
. Vad är då
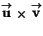 ?
?
a) (9,3,-5) b) (1,1,1) c) (-9,-3,1) d) (18,6,-10) e) (1,-2,1)
- Man vet att
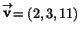 och att
och att
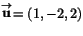 . Vad är den ortogonala
projektionen av
. Vad är den ortogonala
projektionen av
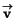 längs
längs
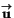 ?
?
a) (2,-4,4) b) (-1,2,-2) c) (3,-6,6) d) (4,6,22) e) (-2,-3,-11)
- Man har punkterna P=(1,3,5), Q=(2,-1,-4) och
R=(-3,1,2). Vad är S om
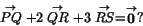
a) (0,0,1) b) (1,0,1) c) (1,1,0) d) (0,1,1) e) (1,0,0)
- Området i figuren, som begränsas uppåt av
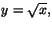 roterar
runt x-axeln så att man får en kropp. Vad är kroppens volym?
roterar
runt x-axeln så att man får en kropp. Vad är kroppens volym?
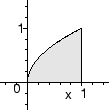
a)
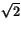 b)
b) 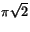 c)
c) 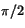 d)
d) 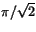 e) 1/2.
e) 1/2.
- När en tunn inhomogen metallstång av längd 1 m placeras längs
positiva x-axeln med ena änden i origo ges densiteten i x av
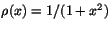 kg/m. Vilken massa har stången?
kg/m. Vilken massa har stången?
a)
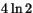 b) 4/17 c) 4 d)
b) 4/17 c) 4 d) 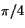 e)
e) 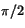
- Vad är masscentrum (tyngdpunkten) av den tunna homogena
kvartscirkelskivan i figuren ?
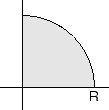
a)
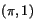 b)
b)
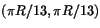 c) (R/13,R/13) d)
c) (R/13,R/13) d)
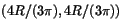 e)
e)
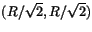
- En 10 m lång kätting med densiteten 2 kg/m hänger ned från en
ställning 15 m över marken. Vilket (minsta) arbete krävs för att dra
upp den? (g är tyngdaccelerationen, alternativen har sorten joule)
a) 100g b) 200g c) 200g2 d) 200 e) 152g
- En av figurerna nedan illustrerar riktningsfältet till
differentialekvationen
y'=y/(1+x2). Vilken?
a) ![\includegraphics [scale=1]{fig3a.ps}](img23.gif)
b) ![\includegraphics [scale=1]{fig3b.ps}](img24.gif)
c) ![\includegraphics [scale=1]{fig3c.ps}](img25.gif)
d) ![\includegraphics [scale=1]{fig3d.ps}](img26.gif)
e) ![\includegraphics [scale=1]{fig3e.ps}](img27.gif)
- Man vet att y(x) löser differentialekvationen
y'=y/(1+x2) och att y(0)=1. Vad är y(1)?
a)
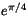 b)
b) 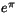 c)
c) 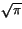 d)
d) 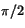 e)
e)
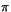
- Man vet att y(x) löser differentialekvationen y'-2xy=2x3
och att y(0)=-1. vad är y(-1)?
a) 3 b) -2 c) -3 d) 2 e) 1
- Den parametriserade kurvan (x(t),y(t)) löser systemet
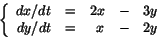
och går genom (4,2) när t=0. Vilken av följande vektorer har en riktning som bäst stämmer överens med hastighetens vid tiden t=1?a) (3,1) b) (2,-1) c) (1,1) d) (1,2) e) (2,3)
Jan-Alve Svensson
2002-11-22