Kompletteringar för Envariabelanalys del B på I
- Talföljder
- Allmänt om serier
- Positiva serier
- Allmänna serier
- Potensserier
- Derivering av potensserier
- Några ''välkända'' serier
- Taylorpolynom och approximation
Talföljder
En talföljd (eller följd eller sekvens av tal) är en oändlig uppräkning av reella tal:Observera att det inte finns något krav på att talen i uppräkningen ska vara olika.
Exempel 1.1
Följden
 är en talföljd.
är en talföljd.
Ett sätt att ange en talföljd är att, som ovan, räkna upp de första talen och
sedan hoppas att läsaren förstår fortsättningen. Ett annat är att ge
en definition av det n:te talet i följden. Exempelvis kan man ange en
följd genom att säga att pn är det n:te primtalet i
storleksordning. Ett annat exempel får man om man sätter
an=1/n, där
Definition 1.1
En talföljd an är konvergerar mot ett tal A, om
det för varje  finns ett heltal N med egenskapen att
finns ett heltal N med egenskapen att
 när
när  .
.
Man skriver då
Exempel 1.2
Följden an=1-1/n är växande och uppåt begränsad av 1, medan följden
an=-n är avtagande, uppåt begränsad av 0 men inte nedåt begränsad.
Sats 1.1
Varje uppåt begränsad växande talföljd är konvergent.
På samma vis är varje nedåt begränsad avtagande följd konvergent.
Bevis. Låt an beteckna talföljden. Mängden av tal som ingår
i den är uppåt begränsad och har därför en minsta övre begränsning
a. Varje omgivning till a innehåller något tal ur talföljden,
eftersom a är den minsta övre begränsningen. Låt an0
vara ett sådant. Eftersom följden är växande gäller att
Allmänt om serier
När an är en talföljd kallas uttrycketför en serie. Serien här börjar med index i=0, men det är inte nödvändigt. När inga missförstånd anses kunna uppstå skrivs vänstra ledet ovan ofta
Men, vad ska egentligen likheten i detta betyda? Vad betyder det att summera oändligt många termer? Till serien
Den femte partialsumman till
Definition 2.1
En serie
 är konvergent om följden av dess partialsummor
är konvergent om följden av dess partialsummor
 är konvergent. Annars är den divergent.
är konvergent. Annars är den divergent.
Om serien är konvergent och gränsvärdet av partialsummorna är S
säger vi att seriens summa är S och skriver
![\framebox [16cm]{\parbox[t]{15cm}{
Serien $\sum_{i}x^{i}$
är konvergent med s...
...{i}=\frac{1}{1-x} \end{displaymath}när $\vert x\vert<1$\ och divergent annars.}}](img29.gif)
Exempel 2.1
Serien
 är konvergent.
är konvergent.
Dess partialsummor Sn bildar en växande följd av tal som är uppåt
begränsad. Vi har nämligen (se figuren nedan)
Vi har därmed sett att seriens summa har mening, men inte lyckats beräkna den. Att summan blir
![\includegraphics [scale=1]{fig1.ps}](img33.gif)
Sats 2.1
Om serien
 är konvergent, så gäller att
är konvergent, så gäller att
 när
när
 .
.
Bevis. Om Sn betecknar seriens n:te partialsumman, så vet
vi att följden Sn har ett gränsvärde S, när
när
Exempel 2.2
Serien
 är divergent, eftersom
är divergent, eftersom  saknar
gränsvärde när
saknar
gränsvärde när
 .
.
Exempel 2.3
Serien
 är divergent trots att
är divergent trots att
 när
när
 .
.
Seriens partialsummor bildar en
växande följd som inte är uppåt begränsad:
Eftersom
Sats 2.2
Om
 är en alternerande serie där
an>0 är en följd som avtar mot 0, så är serien konvergent.
är en alternerande serie där
an>0 är en följd som avtar mot 0, så är serien konvergent.
Bevis. Vi har
så de udda partialsummorna bildar en växande följd. Den är uppåt begränsad eftersom
Låt S vara gränsvärdet av dessa udda partialsummor när
Exempel 2.4
Serien
 är konvergent eftersom den är
alternerande och följden 1/n avtar mot 0.
är konvergent eftersom den är
alternerande och följden 1/n avtar mot 0.
Positiva serier
Det kan kännas nedslående att det är svårt att beräkna seriers summor även om vi vet att de är konvergenta. Men det är tillräckligt intressant att kunna avgöra om en serie konvergerar eller divergerar för att det ska vara mödan värt att systematisera frågan.Jämförelsekriterier
Sats 3.1 (integralkriteriet)
Antag att det finns en avtagande kontinuerlig funktion f(x)>0, så att
f(n)=an. Då är
 och
och
 antingen båda konvergenta eller båda divergenta.
antingen båda konvergenta eller båda divergenta.
Bevis Antag först att integralen konvergerar. Om vi delar in
intervallet [1,n] i n lika stora delar så är
Sn-a1, där Sn är n:te partialsumman till serien,
samtidigt högersumman till
vilket ger
![\framebox [16cm]{\parbox[t]{15cm}{
Serien \begin{displaymath}\sum_{i=1}^{\infty...
...i^{p}}\end{displaymath}
är konvergent när $p\leq1$\ och divergent när $p> 1$}}](img59.gif)
Man jämför serien med
Sats 3.2 (Jämförelsekriteriet)
Antag att
 och
och  är positiva serier med
är positiva serier med
 för alla n. Om
för alla n. Om  är divergent så
är
är divergent så
är  divergent. Om
divergent. Om  är konvergent så
är
är konvergent så
är  konvergent.
konvergent.
Bevis. Låt Sn och Tn beteckna partialsummorna till
Exempel 3.1
Serien
 är konvergent.
är konvergent.
Vi jämför med
Sats 3.3 (Kvotkriteriet)
Låt  vara en positiv serie, sådan att an+1/an
har ett gränsvärde L, när
vara en positiv serie, sådan att an+1/an
har ett gränsvärde L, när
 . Om
L<1 är serien divergent. Om L>1 är den divergent. Ingen slutsats
kan dras om L=1.
. Om
L<1 är serien divergent. Om L>1 är den divergent. Ingen slutsats
kan dras om L=1.
Bevis. Vi ska jämföra serien med en geometrisk serie. Antag först
att
Eftersom r<1 är den geometriska serien
Exempel 3.2
Avgör för vilka a>0, som
 är konvergent.
är konvergent.
Med an=an/n har vi
an+1/an= an/(n+1) som har
gränsvärdet a, när
Exempel 3.3
Serien
 är konvergent och
är konvergent och
 när
när
 .
.
De två senaste exemplen illustrerar att ingen slutsats kan dras när L=1.
Allmänna serier
En serie
Sats 4.1
Om  är absolutkonvergent, så är den också konvergent.
är absolutkonvergent, så är den också konvergent.
Bevis. Tricket är att skriva serien som en skillnad av två
konvergenta positiva serier. Vi har
an=|an|-(|an|-an), så
Båda serierna i högra ledet är positiva och den första är konvergent enligt antagandet. För den andra har vi |an|-an<2|an|, så jämförelsekriteriet ger att även denna är konvergent.
Exempel 4.1
Serien
 som varken är alternerande eller
positiv, är konvergent eftersom den är absolutkonvergent.
som varken är alternerande eller
positiv, är konvergent eftersom den är absolutkonvergent.
En serie som är konvergent men inte absolutkonvergent sägs vara
betingat konvergent. Ett exempel på en sådan är den
alternerande serien
Potensserier
En serie av formen
Sats 5.1
Antag att
 konvergerar för x=x0. Då är
serien (absolut)konvergent när |x|<|x0|.
konvergerar för x=x0. Då är
serien (absolut)konvergent när |x|<|x0|.
Om vi ersätter x med x-a i serien ser vi att om
Sats 5.2
Om
 när
när
 så har
potensserien
så har
potensserien
 konvergensradien R=1/L.
konvergensradien R=1/L.
Här ska 1/L tolkas som
Exempel 5.1
För vilka x konvergerar potensserien
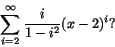
Vi har här att
|an+1/an|=(1+1/n)(n2-1)/(n2+2n), som har
gränsvärdet L=1, när
Exempel 5.2
Bestäm konvergensradien till
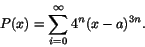
Observera att i detta exempel är bara var tredje koefficient
Exempel 5.3
Bestäm konvergensradien till
 där
där
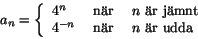
Även här saknar an+1/an gränsvärde. Vi löser problemet genom
att skriva P(x) som en summa av två potensserier.
Här har
Derivering av potensserier
Som tidigare nämnts kan vi tänka på potensserier som ett tillskott till vårt förråd av funktioner. Det blir därför naturligt att fråga om sådana funktioner är deriverbara och om vi kan bestämma primitiva funktioner till dem. Det visar sig att potensserier går utmärkt att derivera (inom sina konvergensradier). I själva verket går de att derivera hur många gånger som helst! För att förstå detta kan man använda följande sats upprepade gånger.
Sats 6.1 (Termvis derivering)
Antag att
 har konvergensradie
R>0. Då är P(x) deriverbar när |x|<R och
har konvergensradie
R>0. Då är P(x) deriverbar när |x|<R och
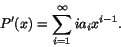
Satsen innehåller (bland annat) påstendet att högra ledet i likheten
ovan konvergerar när |x|<R. Den ''termvisa derivatan'' har alltså en
konvergensradie som är minst lika stor som den ursprungliga
potensserien.
Genom att ersätta x med x-a ser vi att vi också kan derivera
när
Exempel 6.1
Vi har
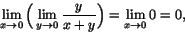
men
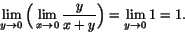
Vi delar upp beviset i tre steg.
men
Lemma 6.1 (Steg 1)
Om
 har konvergensradien R>0, så är
har konvergensradien R>0, så är
 (absolut)konvergent när |x|<R.
(absolut)konvergent när |x|<R.
Genom upprepad användning ser vi att även
Eftersom 0< r<R är
har gränsvärdet 0, när
Lemma 6.2 (Steg 2)
När  finns det ett tal b mellan x och x+h, så att
finns det ett tal b mellan x och x+h, så att
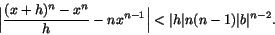
Bevis.
Medelvärdessatsen ger ett a mellan x och x+h, så
att
Samma sats ger ett b mellan x och a (och alltså mellan x och x+h), så att
Eftersom a ligger mellan x och x+h har vi |x-a|<|h|, och påståendet följer. Bevis av sats 6.1 Antag att |x|<R och välj ett r så att |x|<r<R. Vi kan förutsätta att h är så litet att |x|+|h|<r. Av detta följer att alla tal mellan x och x+h har absolutbelopp <r. Vi
och från steg 2 har vi nu att
Tillsammans ger detta
Den sista serien är konvergent (och oberoende av h) enligt steg 1. Vi ser tillsist att
Några ''välkända'' serier
Vi ska nu se att slitet i förra avsnittet var mödan värt. De mest fantastiska samband kommer att uppenbara sig! Vi kommer t.ex. att kunna räkna ut![\framebox [16cm]{\parbox[t]{15cm}{
\begin{displaymath}\sum_{i=0}^{\infty}\frac{x^{i}}{i!}=e^{x}\mbox{ för alla $x$}\end{displaymath}
}}](img134.gif)
Vi låter
![\framebox [16cm]{\parbox[t]{15cm}{
\begin{displaymath}\sum_{i=0}^{\infty}\frac{(-1)^{i}x^{2i}}{2i!}=\cos(x)\mbox{ för alla $x$}\end{displaymath}
}}](img141.gif)
Derivering av detta ger
![\framebox [16cm]{\parbox[t]{15cm}{
\begin{displaymath}\sum_{i=0}^{\infty}\frac{(-1)^{i}x^{2i+1}}{(2i+1)!}=\sin(x)\mbox{ för alla $x$}\end{displaymath}
}}](img143.gif)
För att komma vidare behöver vi en konsekvens av sats 6.1 av generell karaktär.
Sats 7.1 (Termvis integration)
Om
 har konvergensradie R, så är
har konvergensradie R, så är
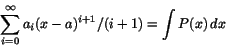
när |x-a|<R.
Bevis.
Det räcker att visa att derivatan av vänstra ledet blir P(x). För
att få påståendet om giltigheten att stämma måste vi visa att serien i
vänstra ledet är (absolut)konvergent när |x-a|<R, dvs att
konvergensradien inte minskar vid termvis integration.
Vi har att P(x) är absolutkonvergent när |x-a|<R. Sätt
när |x-a|<R.
är även Q(x) absolutkonvergent när |x-a|<R. Vi har
![\framebox [16cm]{\parbox[t]{15cm}{
\begin{displaymath}\sum_{i=0}^{\infty}(-1)^...
...r }\vert x\vert<1,\end{displaymath}
eftersom resultatet stämmer när $x=0$.
}}](img151.gif)
Taylorpolynom och approximation
Idén är att försöka approximera en funktion f(x) med ett polynom pn(x) i närheten av en punkt x=a. Vi ska försöka göra detta genom att låta pn(x) ha samma derivator upp till ordning n som f(x) i x=a. Detta polynom kallas taylorpolynomet av grad n till f(x) i punkten a. Samtidigt ska vi försöka hålla reda på vilket fel som uppstår när f(x) ersätts med pn(x). Eftersom derivatorna ska stämma upp till ordning n ser vi genast attProblemet som kvarstår är att förstå skillnaden mellan f(x) och pn(x); hur väl approximerar polynomet funktionen?
Sats 8.1
Antag att f(x) har kontinuerlig derivata av ordning n+1 i en
omgivning till a . När x ligger i denna omgivning gäller då att
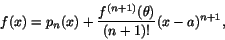
för något tal mellan x och a.
mellan x och a.
Bevis. Beviset bygger på upprepad partiell integration. Låt x
vara fixt.
för något tal
![\begin{eqnarray*}
f(x)-f(a)&=&\int_{a}^{x}f'(t)\,dt=\\
&=&[-(x-t)f'(t)]_{a}^...
...f^{(3)}(t)]_{a}^{x}+\int_{a}^{x}((x-t)^{3}/3!)f^{(4)}(t)\,dt\\
\end{eqnarray*}](img155.gif)
Upprepning ger nu
Enligt förutsättningen är f(n+1) kontinuerlig mellan a och x och antar därför ett största värde M och ett minsta värde m i intervallet mellan a och x, så att
åtminstone om vi förutsättet att x>a eller om n är jämnt. När x<a och n är udda får vi istället omvända olikheter. Integration mellan a och x ger nu
eller omvända olikheter. Division med I=(x-a)n+1/(n+1)! ger nu i båda fallen olikheterna
Enligt satsen om mellanliggande värden finns nu ett
Jan-Alve Svensson
2002-11-25