Lösning av TMA305 Envariabelanalys I, del B,
02 12 14
-
a) Vi ser att y=0 och y=1 är lösningar. Antag därför att
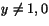 och att x>0. Division ger (separation av variabler)
och att x>0. Division ger (separation av variabler)
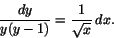
Eftersom
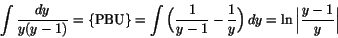
och
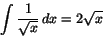
ger integration
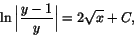
där C är en godtycklig konstant. Exponentiering och bortagning av absolutbelopp ger
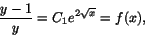
där C1 är en godtycklig konstant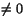 . Omskrivning ger
. Omskrivning ger
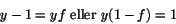
Division ger sedan
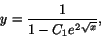
där vi ser att vi även kan välja C1=0, som ger y=1.
Svar: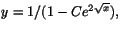 där C är godtycklig,
samt y=0, för alla x.
där C är godtycklig,
samt y=0, för alla x.
b) Division ger
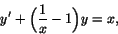
som har den integrerande faktorn
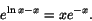
Multiplikation med denna ger
D(xe-xy)=x2e-x,
som integreras till
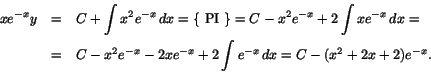
Division ger nu
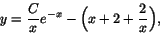
där C är en godtycklig konstant.
Svar: y=(C/x)e-x-(x+2+2/x), där C är godtycklig - Rad 1 ger y=2x-x', som i rad 2 ger
2x'-x''=x+2(2x-x') eller
x''-4x'+5x=0,
som har den karaktäristiska ekvationen med r2-4r+5=0 med rötterna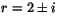 . Lösningarna till (1) är
alltså
. Lösningarna till (1) är
alltså
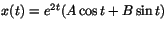 . Eftersom x(0)=0 och
x'(0)=2x(0)-y(0)=-1 får man
. Eftersom x(0)=0 och
x'(0)=2x(0)-y(0)=-1 får man
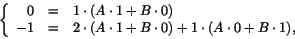
eller A=0, B=-1, så
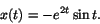
Härav får man
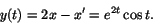
Svar: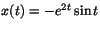 och
och
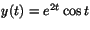 .
.
-
a) Följden
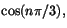
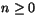 är
är
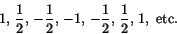
Man ser att kvoten mellan ett tal och dess omedelbara föregångare är 1/2, -1 eller 2. Sätter vi
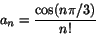
har man
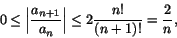
som går mot 0, när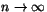 . Potensseriens konvergensradie är alltså
. Potensseriens konvergensradie är alltså 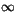 .
.
Svar: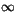 .
.
b) Med an som ovan har man att
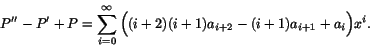
Koefficienten framför xn i detta är
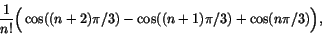
men från beskrivningen av följden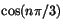 ovan ser man att
detta är 0. Detta visar att P''-P'+P=0.
ovan ser man att
detta är 0. Detta visar att P''-P'+P=0.
c) Ekvationen y''-y'+y=0 har den karaktäristiska ekvationen r2-r+1=0 med lösningarna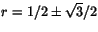 . Ekvationen har
alltså lösningarna
. Ekvationen har
alltså lösningarna
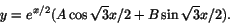
Eftersom P(0)=1 och P'(0)=1/2 får vi
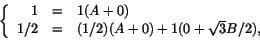
som ger A=1 och B=0. Man får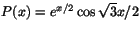 .
.
Svar: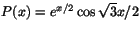 .
.
Svar: Ja
7. Den geometriska serien ger
Substitueras x med -x2 får man
som är Taylorserien kring 0. Taylor polynomet av ordning 6 kring 0 är därför
p6=1-x2+x4-x6.
Svar: p6=1-x2+x4-x6
8. Sätt P=(1,1,1), Q=(2,2,3) och R=(1,2,3) och låt d vara avståndet mellan R och linjen genom de två övriga punkterna. Parallellogramen som spänns av
ger detta
så
Svar:
9. Ett snitt med ett plan genom x på x-axeln vinkelrätt mot denna ger som snitt med kroppen en cirkelskiva med radie 1+x2. Arean av denna är
Skivformeln ger nu att volymen är
Svar:
10. Sätt P=(1,2,1), Q=(2,3,2) och R=(1,4,p). Då är
Parallellogramen som spänns av dessa har area
Eftersom
så får man
(p-3)2+(1-p)2+4=8.
Detta ger 2p2-8p+14=8, som har lösningarna p=1 och p=3.
Svar: p=1 och p=3
11. Sätt
som går mot 1/2, när
Svar: När
Jan-Alve Svensson
2002-12-14