| 1. |
Division ger separation av variabler:
 = = Integration av detta ger
för någon konstant C. Multiplikation med 2 och exponentiering ger sedan
1 + y2 = De-2 sin(1/x),
där D är en positiv konstant.
Villkoret
y(2/
Svar:
y = ±
| ||||
| 2. |
Första ekvationen ger y = - x' + x, som insatt i den andra ger
- x'' + x' = - 3x' + 4x eller
x'' - 4x' + 4x = 0. Denna ekvation har den
karaktäristiska ekvationen
0 = Detta ger x(t) = (A + Bt)e2t, för lämpliga tal A och B. Vi set att x(0) = 1 och från den första ekvationen i systemet också att x'(0) = 1 + 0 = 1. Detta ger oss villkoren A = 1 och B = - 1, så x(t) = (1 - t)e2t Från y = - x' + x får vi nu y(t) = te2t. Svar: x(t) = (1 - t)e2t och y(t) = te2t.
| ||||
| 3. |
| ||||
| 4. |
| ||||
| 6. |
Planets ekvation är
0 = (1, 2, 3) . (x, y - 1, z + 2).
Insättning av (1, 1, 1) ger 0 = 10 vilket inte stämmer så punkten ligger inte i planet. Svar: Punkten ligger inte i planet
| ||||
| 7. |
Man har
cos(t) = 1 - t2/2! + t4/4! -..., kring t = 0. För
t = 2x får vi
Taylorpolynomet
1 - 2x + 2x4/3 för cos(2x) kring x = 0.
Svar: 1 - 2x + 2x4/3.
| ||||
| 8. |
Punkten (4, 0, 0) ligger i planet. Avståndet ges av längden av
den ortogonala projektionen av vektorn (1 - 4, 1, 1) längs normalen
(1, 2, 3). Denna längd är
 = =
Svar:
2/
| ||||
| 9. |
Volymen ges enligt skivformeln av
Svar:
| ||||
| 10. |
Den homogena ekvationen y'' - y = 0 har den karaktäristiska
ekvationen
Ansättning med y = a + bx + cx2 och insättning i den inhomogena ekvationen ger 2c - a - bx - cx2 = x2, så c = - 1, b = 0 och a = - 2, dvs yp = - (2 + x2). Lösningen är alltså av formen y = Aex + Be-x - (2 + x2). Villkoren y(0) = y'(0) = 1 ger nu A + B - 2 = 1 och A - B = 1, så A = 2 och B = 1. Svar: y(x) = 2ex + e-x - (2 + x2).
| ||||
| 11. |
Potensseriens konvergensradie är R = 1/L, där L är gränsvärdet
(när
k
som är 1. Detta ger att serien konvergerar när -1 < x < 1. När x = 1 är serien alternerande och avtagande och därför konvergent.
När x = - 1 är serien
Svar:
-1 < x |
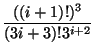
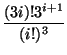 =
= 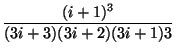 =
= 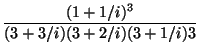 .
.
 =
=  =
=