Veckoblad 1
Under första läsveckan går vi igenom vektorer. Materialet finns i boken avsnitt 13.1-4 samt i avsnitt 12.1 (koordinatsystem i rummet och avstånd mellan punkter i rummet). Förutom själva vektorerna är begreppen skalärprodukt av vektorer och kryssprodukt av vektorer i rummet särskilt viktiga.
Följande uppgifter kommer att gås igenom under lektionerna tisdagen den 5 november:
1) Ett plan i rummet går genom de tre punkterna ( 1, 2, 3) , ( 3, 1, 2) och ( 4, -2, -1) . Bestäm en ekvation för planet.
2) En linje i rummet går genom ( -1, 1, 2) och ( 4, -2, 3) . Bestäm (det kortaste) avståndet från punkten ( 1, 2, 2) till linjen.
3) I en tetraeder är tre av sidoyterna med areorna A, B och C parvis vinkelräta och den fjärde (sneda) sidoytan har arean D . Bevisa att D2 = A2 + B2 + C2 .
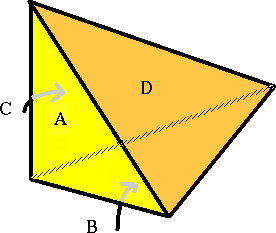
Försök själv lösa uppgifterna innan de tas upp på lektionen!
Jan Alve Svensson <janalve@math.chalmers.se> Last modified 2002-10-29 at 13:02 by Jan Alve Svensson, janalve@math.chalmers.se