Envariabelanalys I, del b, H02
 

Veckoblad 2

Måndagen den 4 november tillämpade vi kryssprodukter och skalärprodukter på problemet att bestämma olika avstånd. Detta står inte i kursboken.

Avstånd mellan punkt och plan

Antag att ett plan har normal $\stackrel{\rightarrow}{\mathbf n}$ och går genom punkten P. Vi vill bestämma (det kortaste) avståndet d mellan punkten Q=(x,y,z) och planet.
 

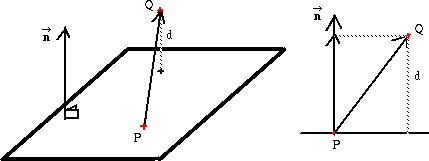
Det ges av längden av den ortogonala projektionen av vektorn $\stackrel{\rightarrow}{PQ}$ längs normalen $\stackrel{\rightarrow}{\mathbf n}$.

Med symboler blir detta

$$d=\frac{\vert\stackrel{\rightarrow}{\mathbf n}\cdot\stackrel... ...}\vert}{\vert\vert\stackrel{\rightarrow}{\mathbf n}\vert\vert}$$

Exempel Bestäm avståndet mellan punkten (1,2,3) och planet x-2y-2z+4=0.

Här ges normalen av (t.ex.) $\stackrel{\rightarrow}{\mathbf n}=(1,-2,-2),$ med längd 3, och (t.ex.) P=(0,2,0) är en punkt i planet. Vi får då $\stackrel{\rightarrow}{PQ}=(1,0,3),$ om vi sätter Q=(1,2,3).

Detta ge oss att avståndet är $\vert(1,0,3)\cdot (1,-2,-2)\vert/3=5/3$.

Avstånd mellan punkt och linje

Antag att en linje i rummet har riktningsvektor $\stackrel{\rightarrow}{\mathbf v}$ och går genom P. Vi vill bestämma (det kortaste) avståndet d mellan linjen och en punkt Q=(x,y,z).
 

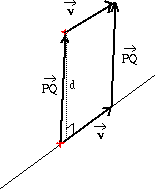
Parallellogrammen som spänns av vektorerna $\stackrel{\rightarrow}{\mathbf v}$ och $\stackrel{\rightarrow}{PQ}$ har area $\vert\stackrel{\rightarrow}{\mathbf v}\times \stackrel{\rightarrow}{PQ}\vert$ men också $d\vert\stackrel{\rightarrow}{\mathbf v}\vert$. Detta ger

$$d=\frac{\vert\stackrel{\rightarrow}{\mathbf v}\times \stackr... ...tarrow}{PQ}\vert}{\vert\stackrel{\rightarrow}{\mathbf v}\vert}$$

Exempel Bestäm avståndet mellan punkten (1,2,3) och linjen som går genom de båda punkterna (1,1,0) och (2,-1,2).

Linjens båda punkter ger oss riktningsvektorn $\stackrel{\rightarrow}{\mathbf v}=(1,-2,2)$ av längd 3. Om vi sätter P=(1,1,0) och Q=(1,2,3) har vi $\stackrel{\rightarrow}{PQ}=(0,1,3)$ och

$$\stackrel{\rightarrow}{\mathbf v}\times\stackrel{\rightarrow... ...y}{rrr} 1 & -2 & 2\\ 0 & 1 & 3 \end{array}\right\}=(-8,-3,1),$$

som har längd $\sqrt{74}$, så avståndet blir $\sqrt{74}/3$.

Avstånd mellan två linjer

Antag att vi har två linjer i rummet med riktningsvektorer $\stackrel{\rightarrow}{\mathbf u}$ respektive $\stackrel{\rightarrow}{\mathbf v}$ och att de går genom P respektive Q.
 

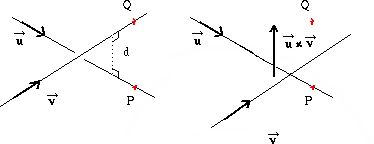
Det kortaste avståndet d mellan de båda linjerna ges då (t.ex.) av avståndet mellan punkten Q och planet genom P med normal $\stackrel{\rightarrow}{\mathbf u}\times\stackrel{\rightarrow}{\mathbf v}$. Vi kan alltså formlera om problemet till att vara avståndet mellan en punkt och ett plan. Vi har

$$d=\frac{\vert\stackrel{\rightarrow}{PQ}\cdot(\stackrel{\righ... ...\mathbf u}\times\stackrel{\rightarrow}{\mathbf v}\vert\vert}.$$

Täljaren kan här beräknas som en 3 x 3-determinant, men det är inte mycket mening med det eftersom kryssprodukten behövs i nämnaren.

Exempel Bestäm avståndet mellan linjen med parameterframställningen (x,y,z)=(1,2,0)+t(1,2,-2) samt linjen genom de två punkterna (3,-2,1) och (1,0,2).

Den första linjen har riktningsvektorn $\stackrel{\rightarrow}{\mathbf u}=(1,2,-2)$ och går genom P=(1,2,0), medan den andra har riktningsvektorn $\stackrel{\rightarrow}{\mathbf v}=(1-3,0-(-2),2-1)=(-2,2,1)$ och går genom Q=(1,0,2). Vi har $\stackrel{\rightarrow}{PQ}=(0,-2,2)$ och

$$\stackrel{\rightarrow}{\mathbf u}\times\stackrel{\rightarrow... ...rrr} 1 & 2 & -2\\ -2 & 2 & 1 \end{array}\right\}=(6,-3,6),$$

så $\stackrel{\rightarrow}{PQ}\cdot(\stackrel{\rightarrow}{\mathbf u}\times\stackrel{\rightarrow}{\mathbf v})=0\cdot 6+ (-2)(-3)+2\cdot3=12.$ Eftersom $\stackrel{\rightarrow}{\mathbf u}\times\stackrel{\rightarrow}{\mathbf v}=\sqrt{36+9+36}=9,$ har vi att avståndet är 12/9=4/3.

Resten av veckan kommer att ägnas åt exempel på tillämpningar av integraler inom fysik, ekonomi och sannolikhetslära.
 

Följande uppgifter kommer att gås igenom under lektionerna tisdagen den 12 november.

1) Beräkna volymen av den kropp (en doughnut) som uppstår när cirkelskivan i figuren roterar kring  x-axeln.
 

 
2) Beräkna masscentrum i den perfekta glasstruten i figuren.
 

 
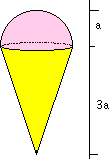
3) Beräkna längden av kurvan  y = cosh( x) , när  x  ligger mellan  -1  och  1 .
 
Försök själv lösa uppgifterna innan de tas upp på lektionen.