Veckoblad 4

 
Den fjärde läsveckan avslutas med metoder att lösa inhomogena linjära differentialekvationer av ordning 2 (med konstanta) koefficienter. Dessa behandlas inte i kursboken. Nödvändigt material och extra uppgifter finns nedan. På övningarna tisdagen den 26 november kommer vi att gå igenom valda uppgifter från duggan som går den lördagen den 23 november. Det blir därför inga veckouppgifter denna vecka.
 
Läsvecka fem ägnas åt talföljder och serier.
 

Den inhomogena ekvationen y''+ay'+by=h(t)

Antag att f(t) och g(t) är två (partikulär-)lösningar till ekvationen. Deras skillnad f(t)-g(t) är då en lösning till den homogena ekvationen y''+ay'+by=0. Om y_h betecknar den allmänna lösningen till denna ser vi att en strategi för att lösa differentialekvationen y''+ay'+by=h(t) är följande.

1. Hitta på något sätt en partikulärlösning y_p till ekvationen.
2. Bestäm allmänna lösningar y_h till motsvarande homogena ekvation y''+ah'+by=0.
3. Den allmänna lösningen till den givna inhomogena ekvationen är nu y=y_p+y_h.

Eftersom vi klarar steg 2, så är det som återstår för att fullständigt lösa y''+ay'+by=h(t) att hitta en enda lösning y_p. En sådan lösning kan ibland hittas med en lämplig typ av ansats. Vi ger först några exempel och formulerar sedan några riktlinjer.

Exempel 1   Lös differentialekvationen y''-y=t.

Med hjälp av den karakteristiska ekvationen vet vi att motsvarande homogena ekvation

y''-y=0

har lösningen y_h=Ae^t+Be^-t. För att hitta en partikulärlösning konstaterar vi att högerledet i

y''-y=t

är ett förstagradspolynom och chansar på att det finns en lösning som också är ett förstagradspolynom. Vi ansätter därför

y=at+b

och försöker bestämma bestämma a och b, så att vi får en lösning till differentialekvationen. Med y=at+b får vi y'=a och y''=0. Vi sätter in i differentialekvationen och ser att vi vill ha

0-(at+b)=t

för alla t. Genom att identifiera koefficienterna på båda sidor ser vi att vi får en lösning genom att ta a=-1 och b=0. En partikulärlösning y_p är alltså y_p(t)=-t. Detta ger att den fullständiga lösningen till differentialekvationen

y''-y=t

är

y=y_p+y_h=-t+Ae^t+Be^-t

där A och B är godtyckliga konstanter.

Exempel 2   Lös differentialekvationen y''-y=e^2t.

Den tillhörande homogena ekvationen är samma som i föregående exempel så dess lösningar kan vi redan. För att hitta en partikulärlösning ansätter vi y=ae^2t och försöker bestämma a så att vi har en lösning. Då är y'=2ae^2t och y''=4ae^2t. Därför vill vi ha en konstant a så att

4ae^2t-ae²=e^2t

dvs

3ae^2t=e^2t.

Detta inträffar om a=1/3 så en partikulärlösning y_p är därför

$$y_{p}=\frac{e^{2t}}{3}$$

och den allmänna lösningen därmed

$$y=\frac{e^{2t}}{3}+Ae^{t}+Be^{-t}.$$

Exempel 3   Lös differentialekvationen y''-y=t+e^2t.

Här utnyttjar vi våra två föregående exempel. Med y₁=-t och y₂=e^2t/3 gäller enligt de föregående exemplen y₁''-y₁=t och y₂''-y₂=e^2t. Nu sätter vi y_p=y₁+y₂ och ser att

y_p''-y_p=(y₁+y₂)''-(y₁+y₂)=t+e^2t.

Alltså är

$$y_{p}=-t+\frac{e^{2t}}{3}$$

en partikulärlösning till ekvationen. Denna har därför den allmänna lösningen

$$y=-t+\frac{e^{2t}}{3}+Ae^{t}+Be^{-t}.$$

Exempel 4   Bestäm en partikulärlösning till y''-y=e^t.

För att försöka hitta en partikulärlösning ansätter vi y=ae^t. Men detta leder till y''-y=0 så vi kan aldrig få ett a så att y''-y=e^t. Det krävs alltså en annan typ av funktion för att få en partikulärlösning. Ett sätt att försöka förenkla problemet är att införa en ny funktion u genom y=e^tu. Detta leder till att y'=e^tu'+e^tu=e^t(u'+u) och y''=e^t(u''+u')+e^t(u'+u)=e^t(u''+2u'+u). Eftersom detta ger

y''-y=e^t(u''+2u')

så har vi

y''-y=e^t

om

u''+2u'=1.

Här är högerledet en konstant och vi ansätter u' som en konstant eftersom det inte finns något u i vänsterledet. Med u'=a får vi u''=0 och i ekvatioen u''+2u'=1 får vi

0+2a=1

dvs a=1/2. Vi vill alltså ha en funktion u så att u'=1/2. Det får vi genom att ta u=t/2. En partikulärlösning till den ursprungliga differentialekvationen är därför

$$y_{p}=\frac{t}{2}\cdot e^{t}$$

Exempel 5   Bestäm en partikulärlösning till

$$y''-y'-2y=\sin{t}.$$

Derivator av $\sin{t}$ och $\cos{t}$ ger upphov till nya uttryck i $\sin{t}$ och $\cos{t}$. Man kan därför hoppas på att en ansats av typen

$$y=a\sin{t}+b\cos{t}$$

skall kunna ge oss en partikulärlösning. Denna ansats leder till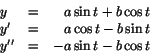

$$\begin{array}{lcr} y&=&a\sin{t}+b\cos{t}\\ y'&=&a\cos{t}-b\sin{t}\\ y''&=&-a\sin{t}-b\cos{t} \end{array}$$

vilket innebär att

$$y''-y'-2y=(-3a+b)\sin{t}+(-3b-a)\cos{t}.$$

Vi har därför en lösning till

$$y''-y-2y=\sin{t}$$

om

$$\begin{array}{rclcl} -3a&+&b&=&1\\ -a&-&3b&=&0 \end{array}$$

Detta system har lösningen a=-3/10 och b=1/10, så en partikulärlösning till differentialekvationen är

$$y=-\frac{3}{10}\, \sin{t}+\frac{1}{10}\, \cos{t}.$$

Av exemplen kan vi dra följande slutsatser om hur man kan försöka hitta partikulärlösningar.

h(t) = polynom	ansätt  y  polynom av samma grad
h(t) = cekt	ansätt  y = aekt
h(t) = csin kt + dcos kt	ansätt  y = asin kt + bcos kt

Dessutom såg vi att man kan bli av med en faktor e^kt i högerledet, genom att införa en ny funktion u genom y=e^ktu.

 
Extra uppgifter
 
Lös följande differentialekvationer.

1. y'' - 4y' + 4y = 2t + 8
2. 0.5y'' + y = t² - 7t + 10
3. y'' - 7y' + 10y = t³
4. y'' + y = e^t
5. y'' + y = sin 2t
6. y'' - 2y' + y = te^t
7. y'' + y = e^-tsin 2t
8. Lös följande så kallade begynnelsevärdesproblem
    
   
   y'' - y = e^t,   y(0) = 2 och y'(0) = 1/2 .

 
Svar

1. y = (t + 5)/2  + (A + Bt)e^2t
2. y = t²-7t + 9 + Asin 2^1/2t + Bcos 2^1/2t
3. y = 0.1t³ + 0.21t² + 0.234t + 0.1218 + Ae^5t + Be^2t
4. y = 0.5e^t + Asin t + Bcos t
5. y = -sin(2t)/3 + Asin t + Bcos t
6. y = (A + Bt + t³/6)e^t
7. y = e^-t(0.2cos 2t-0.1sin 2t) + Asin t + B\cos t
8. y = (1 + 0.5t)e^t + e^-t