Veckoblad 5

 
Under femte läsveckan har vi ägnat oss dels åt talföljder och dels åt serier. Vi har i synnerhet tittat på deras konvergens eller divergens. Fredagen den 29 november kommer vi till så kallade potensserier och deras konvergensradier. Vi går också igenom en sats som finns i det utdelade häftet om derivering av potensserier. Längst ned på denna sida finns tre uppgifter. De två sista kräver sådant som gås igenom på fredagen.
 

Sammanfattning av satser om konvergens
 

1. Om $\sum_{i}a_{i}$ är konvergent, så gäller att $a_{n}\rightarrow 0,$ när $n\rightarrow \infty$. Används för att avslöja divergenta serier.
2. Om f(x)>0 är kontinuerlig och avtagande och a_n=f(n), så är
   
   $$\sum_{i=1}^{\infty}a_{n}\mbox{\hspace{5mm} och \hspace{5mm}}\int_{1}^{\infty}f(x)\,dx$$
   
   
   båda divergenta eller båda konvergenta. Den undre gränsen är inte viktig här!
3. Om $0\leq a_{n}\leq b_{n}$ för alla (stora) n, så är
   1. $\sum_{i=1}^{\infty}a_{n}$ konvergent om $\sum_{i=1}^{\infty}b_{n}$ är det.
   2. $\sum_{i=1}^{\infty}b_{n}$ divergent om $\sum_{i=1}^{\infty}a_{n}$ är det.
   Den nedre gränsen är oväsentlig!
4. Om a_n>0 och a_n+1/a_n har gränsvärdet L, när $n\rightarrow \infty,$ så är
   1. $\sum_{i=1}^{\infty}a_{i}$ konvergent om L<1
   2. $\sum_{i=1}^{\infty}a_{i}$ divergent om L>1.
   Den nedre gränsen är oväsentlig! Observera att ingen slutsats kan dras om L=1 eller om gränsvärdet L inte finns.
5. Om $\sum_{i}\vert a_{i}\vert$ är konvergent, så är $\sum_{i}a_{i}$ konvergent.

   Man kan, i momentet ovan, alltså också arbeta med |a_n+1/a_n|.

6. Om $a_{n}\geq 0$ och följden a_n avtar mot noll, så är $\sum_{i}(-1)^{i}a_{i}$ konvergent.

Uppgifter

 

1. En talföljd ges av att a₀=1/2 och att a_n+1=(a_n+a_n²)/2, när 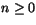$n\geq 0$. (Nästa tal i följden bestäms alltså av sin omedelbara föregångare.)
    
   (a) Visa att 1 är en övre begränsning till följden och att 0 är en undre. (Ledning: antag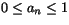 $0\leq a_{n}\leq 1$ och visa att samma sak gäller för a_n+1.)
    
   (b) Visa att följden är avtagande genom att visa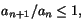 $a_{n+1}/a_{n}\leq 1,$ för alla n.
    
   (c) Argumentera för att följden är konvergent och bestäm dess gränsvärde (när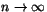 $n\rightarrow \infty$).

2. För vilka x konvergerar serien
   
   $$\sum_{i=1}^{\infty}\frac{(-1)^{n}n}{2^{n}(n^{2}+1)}x^{n}?$$
   
   

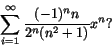
3. Bestäm konvergensradien för serien
   
   $$1+\frac{x^{3}}{3!}+\frac{x^{6}}{6!}+\frac{x^{9}}{9!}+\frac{x^{12}}{12!}+\ldots$$
   
   
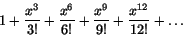
   och visa att den löser
   
   y''+y'+y=e^x.
   
   
   Beräkna seriens summa.