MATEMATIK Chalmers
Linjär algebra och flervariabelanalys I, del B, V02

Tillägg till teorin

Gränsvärden

 

Mängden av punkter i $\Bbb R^{n}$ vars avstånd till en fix punkt  a  är mindre än något fixt tal $\epsilon$ (>0), kallas en omgivning till  a . Med symboler kan en sådan omgivning skrivas
$\{\mathbf{x}\in\Bbb R^{n}\,\vert\,\vert\mathbf{x}-\mathbf{a}\vert<\epsilon\}$.

När n=3 och  a  alltså är en punkt i rummet, består en omgivning av ett klot (där skalet inte ingår) runt  a . När n=2 och  a  alltså är en punkt i planet är en omgivning till  a  en cirkelskiva runt punkten (där periferin inte ingår). När n=1 är den fixa punkten ett tal a och en omgivning till det ett är ett öppet symmetriskt intervall runt a.

Att värdet av en funktion  f(x)  från $\Bbb R^{n}$ till $\Bbb R$ närmar sig talet A när $\mathbf{x}\rightarrow\mathbf{a}$ betyder att det till varje omgivning till  A  finns en omgivning till punkten  a  så att  f:s värden här ligger i den första omgivningen. Detta garanterar att funktionens värden avviker godtyckligt lite från  A  bara variabeln ligger tillräckligt nära  a .

Med hjälp av symbolerna $\epsilon$ respektive $\delta$ för radien i de båda omgivningarna kan detta formuleras

Definition 1 Funktionen  f(x)  har gränsvärdet A, när  x  går mot  a  om det för varje $\epsilon\gt$ (läs: omgivning till  A ) finns ett $\delta\gt$ (läs: omgivning till  a ) så att

$$\vert f(\mathbf{x})-A\vert<\epsilon \mbox{ när } \vert\mathbf{x}-\mathbf{a}\vert<\delta.$$

(Läs: f:s värde i  x  ligger i omgivningen till  A  när  x  ligger i omgivningen till  a .)

Att  f  har gränsvärdet  A  (eller går mot  A ) när  x  går mot  a , skrivs ofta $f(\mathbf{x})\rightarrow A,$ när $\mathbf{x}\rightarrow\mathbf{a},$ eller

$$\lim_{\mathbf{x}\rightarrow\mathbf{a}}f(\mathbf{x}) = A.$$

Det uttrycks också ofta så att $\vert f(\mathbf{x})-A\vert\rightarrow 0,$ när $\vert\mathbf{x}-\mathbf{a}\vert\rightarrow 0$.

Exempel Låt  f(x) = x_i  dvs projektion på den i:te koordinaten. Vi har då att $f(\mathbf{x})\rightarrow a_{i}$ när $\mathbf{x}\rightarrow\mathbf{a},$ där  a_i  är  i:te koordinaten i $\mathbf{a}$. Vi har nämligen att $\vert f(\mathbf{x})-a_{i}\vert=\vert x_{i}-a_{i}\vert\leq \vert\mathbf{x}-\mathbf{a}\vert,$ så att $\vert f(\mathbf{x})-a_{i}\vert\rightarrow 0,$ när $\vert\mathbf{x}-\mathbf{a}\vert\rightarrow 0$.

När man ska undersöka gränsvärdet av  f(x)  då $\mathbf{x}\rightarrow\mathbf{a}$ kan man börja med att låta  x  närma sig  a  på olika enkla sätt, t.ex. längs räta linjer. Får man då inte samma gränsvärde har man redan visat att gränsvärdet inte finns. Får man samma värde  A  får man ordentligt försöka visa att gränsvärdet är  A .

Exempel   Funktionen  f(x,y) = xy/ (x² + y²)  saknargränsvärde när $(x,y)\rightarrow(0,0)$. Om vi närmar oss origo längs linjen  y = kx  (där  k  är någon konstant) får vi  f(x, kx) = k/ (1 + k²)  som har gränsvärdet  k/ (1 + k²) , när $x\rightarrow 0$. Vi får alltså olika gränsvärden längs olika linjer in mot origo, så  f  har inget gränsvärde när $(x,y)\rightarrow(0,0)$.

Även om man får samma gränsvärde längs samtliga räta linjer in mot en punkt betyder det inte att funktionen har ett gränsvärde när  x  närmar sig denna punkt.

Exempel   Funktionen  f(x,y) = y(x²+y²)/ x  är definierad överallt utom längs  y-axeln. Om man närmar sig origo längs linjen  y = kx  får man  f(x,kx) = x²(1 + k²)k , som går mot 0, när $x\rightarrow 0$.

Trots detta saknar funktionen gränsvärde när $(x,y)\rightarrow(0,0)$. Om vi fixerar  r > 0  och undersöker  f:s värden längs cirkeln med radie  r  och medelpunkt i origo ser vi att  f  antar godtyckligt små och godtyckligt stora värden längs cirkeln. Med polära koordinater $x=r\cos(\theta),$ $y=r\sin(\theta),$ har vi nämligen att $f(x,y)=r^{2}\tan(\theta),$ som blir litet när $\theta\gt-\pi/2$ ligger nära $-\pi/2$ och stort när $\theta<\pi/2$ ligger nära $\pi/2$.

Ibland kan man använda envariabelanalysens Taylorutveckling för att bestämma gränsvärden av funktioner av flera variabler.

Exempel   Undersök funktionen  f(x, y) = (cos(x + y) - 1 + xy)/ (x² + y²) när $(x,y)\rightarrow(0,0)$.

Vi har Taylorutvecklingen  cos(t) = 1 - t²/ 2 + t²B(t)  runt  t = 0 , där  B(t)  är en funktion som är begränsad i närheten av  t = 0 . Använder vi detta får vi

$$f(x,y)=\frac{1-(x+y)^{2}/2-1+xy+(x+y)^{4}B(x+y)}{x^{2}+y^{2}}=\frac{-x^{2}/2-y^{2}/2+(x+y)^{4}B(x+y)}{x^{2}+y^{2}}.$$

Övergång till polära koordinater $x=r\cos(\theta),$ $y=r\sin(\theta)$ ger att vi ska undersöka

$$-1/2+r^{2}(\cos(\theta)+\sin(\theta))^{4}B(x+y)$$

när $r\rightarrow 0$. Eftersom  B ,  cos  och  sin  är begränsade blir detta gränsvärde  -1/ 2 . Vi får alltså $f(x,y)\rightarrow -1/2,$ när $(x,y)\rightarrow (0,0).$

Precis som för gränsvärden för funktioner av en variabel gäller följande räkneregler:

Sats 1   Antag att $f(\mathbf{x})\rightarrow A$ och att $g(\mathbf{x})\rightarrow B$ när $\mathbf{x}\rightarrow\mathbf{a}$ och att  c  är en konstant. Då gäller

1.

$cf(\mathbf{x})\rightarrow cA,$

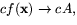
2.

$f(\mathbf{x})+g(\mathbf{x})\rightarrow A+B,$

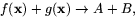
3.

$f(\mathbf{x})g(\mathbf{x})\rightarrow AB,$

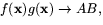
4.

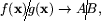$f(\mathbf{x})g(\mathbf{x})\rightarrow AB,$ (om $B\neq 0$)

när $\mathbf{x}\rightarrow\mathbf{a}$.

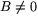Bevis av 2) och 3). Triangelolikheten ger

$$0\leq \vert f(\mathbf{x})+g(\mathbf{x})-(A+B)\vert\leq \vert f(\mathbf{x})-A\vert+\vert g(\mathbf{x})-B\vert.$$

Enligt förutsättningen går båda termerna mot 0, när $\vert\mathbf{x}-\mathbf{a}\vert\rightarrow 0,$ så även högra ledet i första olikheten går mot då.

Omskrivning och triangelolikheten ger

$$\begin{array} {rcl} 0\leq\vert f(\mathbf{x})g(\mathbf{x})-A... ...)-B)\vert+\vert B\vert\vert(f(\mathbf{x})-A)\vert.\end{array}$$

Enligt förutsättningen går $\vert(f(\mathbf{x})-A)\vert$ och $\vert(g(\mathbf{x})-B)\vert$ mot när $\vert\mathbf{x}-\mathbf{a}\vert\rightarrow 0,$ så även högra ledet i första olikheten går mot då.

 

Kontinuitet

 

Definition 2   En funktion  f(x)  från $\Bbb R^{n}$ till $\Bbb R$ är kontinuerlig i punkten  a  om $\lim_{\mathbf{x}\rightarrow\mathbf{a}}f(\mathbf{x})$ existerar och är  f(a) .

Om man nystar upp definitionen av gränsvärde betyder detta att det för varje omgivning till  f(a)  finns en omgivning till  a  som av  f  avbildas in i omgivningen till $f(\mathbf{a})$.

En funktion är kontinuerlig om den är kontinuerlig i varje punkt i sin definitionsmängd.

Exempelvis är den funktion som avbildar  x  på dess i:te koordinat  x_i  kontinuerlig eftersom $\lim_{\mathbf{x}\rightarrow\mathbf{a}}x_{i}=a_{i},$ den i:te koordinaten i  a .

Sats 2   Om  f(x)  och  g(x)  är kontinuerliga i  a  och  c  är en reell konstant så är  cf(x) ,  f(x)  + g(x) ,  f(x)g(x)  och    f(x)/ g(x)  kontinuerliga i  a . (det sista under förutsättning att $g(\mathbf{a})\neq 0$).

Bevis   Följer genast från räknereglerna för gränsvärden.

Exempelvis är varje funktion som definieras av ett uttryck uppbyggt av koordinater och konstanter med hjälp av addition, multiplikation och division kontinuerlig.

Sats 3   Om  f(x)  är kontinuerlig i  a  och  g(t)  (reellvärd funktion av en reellvariabel) är kontinuerlig i  f(x) , så är  g(f(x))  kontinuerlig i  a .

Bevis   Eftersom  g  är kontinuerlig finns det till varje omgivning av  g(f(a))  en omgivning till  f(a)  som  g  avbildar in i den första omgivningen.

Till denna andra omgivning finns sedan, eftersom  f  är kontinuerlig, en (tredje) omgivning till  a  som  f  avbildar in i den andra omgivningen.

Vi får att  g(f(x))  avbildar den tredje omgivningen in i den första. Detta visar satsen.

Exempelvis är  cos(xy)/ arctan(x² +y²)  kontinuerlig överallt utom i origo. Funktionen  cos(xy)  är sammansättningen av de två kontinuerliga funktionerna  f(x, y) = xy  och  cos(t) . På liknande sätt är  arctan(x² +y²)  sammansättning av två kontinuerliga funktioner. Deras kvot är därför kontinuerlig utom där nämnaren är 0, dvs i origo.

Exempel   Undersök om man kan bestämma talet  a  så att funktionen

$$f(x,y)=\left\{ \begin{array} {lcl} y^{2}/(x^{2}+y^{2}) & \... ...,0)\\ a & \mbox{ när } & (x,y)=(0,0)\\ \end{array} \right.$$

blir kontinuerlig överallt.

Av uttrycket framgår att  f  är kontinuerlig utom möjligen i origo. För kontinuitet i origo ska vi ha att gränsvärdet av  y²/ (x² + y²)  när $(x,y)\rightarrow(0,0),$ ska existera och  a  ska sedan väljas som detta gränsvärde. Polära koordinater ger

$$y^{2}/(x^{2}+y^{2})=\sin^{2}(\theta)$$

som inte ger något gränsvärde oberoende av $\theta$ när $r\rightarrow 0$. Gränsvärdet existerar alltså inte och  a  kan inte väljas så att funktionen blir kontinuerlig i origo.

I fallet med en reellvärd funktion  f(x,y)  av två variabler kan man få åskådlig bild av kontinuitet genom att använda grafen till  f . Att  f  är kontinuerlig i  (a, b)  betyder att punkten  (x, y, f(x, y))  närmar sig  (a,b, f(a, b))  när $(x,y)\rightarrow (a,b)$ (i  x,y-planet).

Exempel   Undersök om det går att bestämma talet  a  så att

$$f(x,y)=\left\{ \begin{array} {lcl} y\arctan(xy)/(x^{2}+y... ...0)\\ a & \mbox{ när } & (x,y)=(0,0)\\ \end{array}\right.$$

blir kontinuerlig överallt.

Av uttrycket framgår (med hjälp av satserna ovan) att  f  är kontinuerlig utom möjligen i origo. Taylorutvecklingen av  arctan(t)  i t=0 är  t + . . .  . Vi ser att $\arctan(t)/t\rightarrow 1,$ när $t\rightarrow 0$. Eftersom  xy  är kontinuerlig (i origo) gäller att $xy\rightarrow 0,$ när $(x,y)\rightarrow(0,0)$. Detta ger oss att $\arctan(xy)/xy\rightarrow 1,$ när $(x,y)\rightarrow(0,0)$.

Vi gör därför omskrivningen

$$\frac{xy\arctan(xy)}{(x^{2}+y^{2})^{3/2}}=\frac{x^{2}y^{2}}{(x^{2}+y^{2})^{3/2}}\frac{\arctan(xy)}{xy}$$

Polära koordinater i den första termen ger

$$\frac{x^{2}y^{2}}{(x^{2}+y^{2})^{3/2}}=\frac{r^{4}\cos^{2}(\theta)\sin^{2}(\theta)}{r^{3}}=r\cos^{2}(\theta)\sin^{2}(\theta),$$

som går mot  0  när $r\rightarrow 0,$ eftersom $\cos^{2}(\theta)\sin^{2}(\theta)$ är begränsat.

Räknereglerna för gränsvärden ger nu att $xy\arctan(xy)/(x^{2}+y^{2})^{3/2}\rightarrow 0\cdot 1=0,$ när $(x,y)\rightarrow(0,0)$. Vi ska alltså välja  a = 0 , för att  f  ska vara kontinuerlig även i origo.

 

Differentierbarhet

 

Man kan ha två lite olika förhållningssätt till derivata av en reellvärd funktion av en reell variabel.

Det ena är att derivatan (momentant) mäter funktionens relativa förändring när variabeln ändras. Det andra är att derivatan väsentligen bestämmer tangentlinjen till grafen för funktionen.

När man betraktar funktioner av flera variabler divergerar dessa två förhållningssätt till två olika begrepp.

Det första leder till partiella derivator (och i sin förlängning till riktningsderivator) det andra leder till begreppet differentierbarhet och differential av funktionen.

Från envariabelanalysen vet vi att om en funktion är deriverbar i en punkt är den också kontinuerlig där. Argumentet är enkelt:

$$g(t)-g(a)=\frac{g(t)-g(a)}{t-a}(t-a)\rightarrow g'(a)\cdot 0=0,$$

när $t\rightarrow a,$ som ger att $g(t)\rightarrow g(a),$ när $t\rightarrow 0$.

I kontrast till detta finns det funktioner av två variabler som är partiellt deriverbara i origo men inte kontinuerliga där.

Ett sådant exempel ges av

$$f(x,y)=\left\{ \begin{array} {lcl} xy/(x^{2}+y^{2}) & \mbo... ...0,0)\\ 0 & \mbox{ när } & (x,y)=(0,0).\\ \end{array}\right.$$

För att beräkna  f'_x(0, 0)  ska vi undersöka  (1/ x)(f(x,0) - f(0,0)) = 0  när $x\rightarrow 0,$ så  f'_x(0, 0) = 0 . På samma sätt är  f'_y(0, 0) = 0 .

Å andra sidan ger polära koordinater

$$xy/(x^{2}+y^{2})=\cos(\theta)\sin(\theta),$$

som inte ger något gränsvärde oberoende av $\theta$ när $r\rightarrow 0$. Det är alltså omöjligt att definiera funktionen i origo så att den blir kontinuerlig där.

En annan uppenbar brist hos partiella derivator (utan ytterligare villkor) är att det beror på hur koordinataxlarna väljs. För tillfället tycks de vara helt fel begrepp. (Situationen kommer senare att räddas av ytterligare villkor på dem.)

Vi fullföljer därför det andra förhållningssättet till derivata. Låt oss tänka på fallet med en funktion av två variabler och dess graf. Vi vill att det det ska finnas ett plan genom punkten  (a, b, f(a, b))  som bäst approximerar grafen. Ekvationen för ett sådant plan kan skrivas  z = A(x - a) + B(y - b) + f(a, b) , för några konstanter  A  och  B . När  f  ersätts med  A(x - a) + B(y - b) + f(a, b)  blir felet

 E(x, y) = f(x, y) - f(a, b) - A(x - a) - B(y - a) = f(x, y) - f(a, b) - (A, B)·(x-a, y-b) .

När  f  är kontinuerlig går  E(x, y)  mot noll oavsett hur vi väljer konstanterna  A  och  B . Vi tittar därför på det relativa felet

R(x, y) = E(x, y)/ |(x, y) - (a, b)| = (f(x, y) - f(a, b) - (A,B)·(x-a, y-b))/ |(x, y) - (a, b)| 

Nu är det inte längre klart att det går att välja (A,B) så att uttrycket går mot 0, när $(x,y)\rightarrow (a,b)$.

Definition 3   Funktionen  f(x)  är differentierbar i  a  om det finns en vektor  A  så att det relativa felet

$$R(\mathbf{x})=\frac{f(\mathbf{x})-f(\mathbf{a})-\mathbf{A}\c... ...}-\mathbf{a})}{\vert\mathbf{x}-\mathbf{a}\vert}\rightarrow 0,$$

när $\mathbf{x}\rightarrow\mathbf{a}$.

Man kan undra om  A  kan väljas på flera olika sätt när  f  är differentierbar i  a . Att så inte är fallet visas av

Sats 4   Om  f  är differentierbar i  a så är  f  partiellt deriverbar i  a  och  f_i'(a) = A_i (den i:te koordinaten i  A ).

Bevis   Vi ska undersöka

$$\begin{array} {rcl} (1/t)(f(\textbf{a}+t\textbf{e}_{i})-f(\... ...vert t\vert/t)R(\textbf{a}+t\textbf{e}_{i})+A_{i},\end{array}$$

när $t\rightarrow 0$. När $t\rightarrow 0$ har vi $\textbf{a}+t\textbf{e}_{i}\rightarrow \mathbf{a}$. Eftersom $R(\mathbf{x})\rightarrow 0$ när $\mathbf{x}\rightarrow\mathbf{a}$ och  |t|/ t  är begränsad, blir gränsvärdet  A_i .

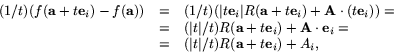
Exempel   Funktionen $f(x,y)=\sqrt{x^{2}+y^{2}}$ är inte differentierbar i origo eftersom den inte är partiellt deriverbar i origo där.

T.ex. skulle  f'_x(0, 0)  vara derivatan till  f(x, 0) = |x| , som ju inte existerar.

Sats 5   Om  f  är differentierbar i  a  så är  f  kontinuerlig i  a .

Bevis   Vi har att $f(\mathbf{x})-f(\mathbf{a})=\vert\mathbf{x}-\mathbf{a}\vert R(\mathbf{x})+\mbox{grad}f(\mathbf{a})\cdot(\mathbf{x}-\mathbf{a})\rightarrow 0+0=0,$ när $\mathbf{x}\rightarrow\mathbf{a}$. Detta visar att $f(\mathbf{x})\rightarrow f(\mathbf{a}),$ när $\mathbf{x}\rightarrow\mathbf{a}$ och därför att  f  är kontinuerlig i  a . .

Differentierbarhet verkar alltså vara helt rätt begrepp. Problemet är att för att säkerställa differentierbarhet behöver vi beräkna ett (komplicerat) gränsvärde.

Situationen räddas av följande sats som också återupprättar de partiella derivatornas anseende.

Sats 6   Antag att  f  har kontinuerliga partiella derivator i en omgivning till  a . Då är  f  differentierbar i  a .

I beviset ska vi använda medelvärdessatsen från envariabelanalysen. Låt  g(t)  vara kontinuerlig i  [a, b]  och deriverbar i  (a, b) . Då finns ett tal  c , a < c < b , så att  g(b) - g(a) = g'(c)(b - a) .

Bevis   Vi genomför beviset bara när  f  har två variabler. Det generella fallet är snarlikt.

Vi ska visa att

$$\begin{array} {l} R(x,y)=\\ \hspace{5mm}=(1/\sqrt{(x-a)^{... ...f(x,y)-f(a,b)-f'_{x}(a,b)(x-a)-f'_{y}(a,b)(y-a))\end{array}$$

har gränsvärdet  0  när $(x,y)\rightarrow (a,b)$.

Envariabelfunktionerna  f(x, y)  för fixt  y  och  f(a, y)  är deriverbara enligt förutsättningen (när  (x, y)  ligger i en omgivning till  (a, b) ). Vi använder medelvärdessatsen och gör omskrivningen

$$\begin{array} {rcl} f(x,y)-f(a,b)&=& f(x,y)-f(a,y)+f(a,y)-f(a,b)=\\ &=& f'_{x}(c,y)(x-a)+f'_{y}(a,d)(y-a)\end{array}$$

för lämpliga tal  c  och  d  mellan  x  och  a  respektive mellan  y  och  b . Observera att  c  och  d  går mot  a  respektive  b  när $(x,y)\rightarrow (a,b)$. Vi får nu

 R(x,y) = 

$$\hspace{5mm}=\frac{x-a}{\sqrt{(x-a)^{2}+(y-b)^{2}}}\Big(f'_{... ...{\sqrt{(x-a)^{2}+(y-b)^{2}}}\Big(f'_{y}(a,d)-f'_{y}(a,b)\Big),$$

där  f'_x(c, y) - f'_x(a, b)  och  f'_y(a, d) - f'_y(a, b)  båda går mot  0  när $(x,y)\rightarrow (a,b)$. Detta använder de partiella derivatornas kontinuitet. Eftersom $\vert x-a\vert/\sqrt{(x-a)^{2}+(y-b)^{2})}$ och $\vert y-b\vert/\sqrt{(x-a)^{2}+(y-b)^{2})}$ båda är $\leq 1$ (nämnaren är $\geq$ täljaren) ger detta att $R(x,y)\rightarrow 0$ när $(x,y)\rightarrow (a,b)$.

Exempel   Funktionen  f(x, y) = (y² - x)/ arctan(xy) är differentierbar överallt:

Dess definitionsmängd är hela planet utom koordinataxlarna. Räknereglerna för derivering ger

$$f'_{x}(x,y)=\frac{-\arctan(xy)-(y^{3}-xy)/(1+x^{2}y^{2})}{\arctan(xy)^{2}}$$

och

$$f'_{y}(x,y)=\frac{2y\arctan(xy)-(xy^{2}-x^{2})/(1+x^{2}y^{2})}{\arctan(xy)^{2}}$$

som båda är kontinuerliga (överallt).

 

Kedjeregeln

 

I många situationer har man anledning att betrakta funktioner av typen  f(x(t), y(t)) , där  f  är en funktion av två variabler som i sin tur beror av  t  (Du kan tänka på  t  som tiden).

En partikels rörelse i planet kan t.ex. beskrivas som  x(t) = (x(t), y(t))  så att man anger vad  x- respektive  y-koordinaterna är vid olika tidpunkter  t . En sådan funktion  f(x(t))  kallas en parametriserad kurva i planet. När  x(t)  har  n  kooridnater talar man om en kurva i $\Bbb R^{n}$. Med derivatan av en sådan parametriserad kurva vid tiden  t  menas  x'(t) = (x₁'(t), . . . , x_n'(t))  Den fysikaliska tolkningen av  x'(t)  är att den anger hastigheten vid tiden  t . Farten vid samma tid är då  |x'(t)| .

Antag att  x(t)  beskriver en partikels rörelse i planet och att  f(x, y)  anger t.ex. temperaturen i punkten  (x, y) . Vi kan då vara intresserade av att veta hur temperaturen ändras momentant vid tiden  t . Temperaturen vid tiden  t  anges av  f(x(t)) , så den momentana temperaturförändringen ges av den vanliga derivatan till denna funktion (som enbart beror på  t ).

Exempel   En partikel rör sig längs enhetscirkeln enligt  x(t) = (cos(t), sin(t)) . Temperaturen i planet är oföränderlig i tiden och ges av  f(x, y) = 2x² - 2xy + 2y² .

Vi har då att  f(x(t)) = 2 - sin(2t) , så den momentana temperaturförändringen vid tiden  t  är  -2cos(2t) .

I flera tillämpningar är det viktigt att använda att derivatan till  f(x(t))  kan uttryckas med hjälp av gradienten  grad f(x(t))  och tangentvektorn  x'(t) . Detta är innehållet i kedjeregeln (envariabelfallet).

Sats 7   (Kedjeregeln, en variabel) Antag att  f  är differentierbar i  x(t))  och att  x(t))  är deriverbar i  t . Då gäller

$$\frac{df}{dt}=\mbox{grad}f(\mathbf{x}(t))\cdot \mathbf{x}'(... ...}+\ldots+\frac{\partial f}{\partial x_{n}}\frac{dx_{n}}{dt}.$$

Anmärkning   I vänstra ledet i kedjeregeln står  f  alltså egentligen för (den sammansatta) funktionen  f(x(t))  som bara beror på den reella variabeln  t . Man får förstå detta ur sammanhanget; eftersom man deriverar med avseende på  t  kan  f  inte stå för  f(x₁, x₂, . . . ,x_n)  som ju beror på de  n  variablerna  x₁, x₂, . . . ,x_n .

Bevis   Vi ska alltså beräkna gränsvärdet  (1/ h)(f(x(t + h) - f(x(t))  när $h\rightarrow 0$.

Med hjälp av det relativa felet  R(x(t+h))  kan detta skrivas

$\frac{1}{h}\vert\mathbf{x}(t+h)-\mathbf{x}(t)\vert R(\mathbf{x}(t+h))+\frac{1}{h}\mbox{grad}f(\mathbf{x}(t))\cdot (\mathbf{x}(t+h)-\mathbf{x}(t))$.

Eftersom  x(t)  är deriverbar och därför kontinuerlig gäller att

$\mathbf{x}(t+h)\rightarrow \mathbf{x}(t),$ när $h\rightarrow 0$.

Deriverbarheten ger också att $\frac{1}{h}(\mathbf{x}(t+h)-\mathbf{x}(t))\rightarrow \mathbf{x}'(t),$ när $h\rightarrow 0$).

Eftersom  f  är differentierbar i  x(t)  får vi nu också att $R(\mathbf{x}(t+h))\rightarrow 0,$ när $h\rightarrow 0$ (för då gäller att $\mathbf{x}(t+h)\rightarrow \mathbf{x}(t)$.

Exempel   Enligt satsen ska alltså den momentana temperaturförändringen i det tidigare exemplet ges av  (4x - 2y)x' + (-2x + 4y)y' , där  x = cos(t)  och  y = sin(t) . Insättning av detta ger  (4cos(t) - 2sin(t))(-sin(t)) + (-2cos(t) + 4sin(t))cos(t) = -2(cos²(t) - sin²(t)) = -2cos(2t) .

Ibland är man intresserad av att betrakta funktioner av formen  f(x(u, v), y(u, v)) , dvs  f  är en funktion av ett antal variabler (i detta fall två), som i sin tur är funktioner av andra variabler (i detta fall två). Som en direkt följd av kedjeregeln kan man beräkna partialderivatorna av  f  (egentligen  f(x(u, v), y(u, v)))  t.ex med avseende på  v . Man får då

$$\frac{\partial f}{\partial u}=\frac{\partial f}{\partial x... ...}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial u}$$

Ett vanligt sätt att använda kedjeregeln är vid lösning av partiella differentialekvationer, dvs ekvationer som involvera partiella derivator av en funktion  f(x, y) . Sådana kan vara mycket svåra att lösa exakt. En metod som kan fungera är att man gör ett så kallat (intelligent) variabelbyte. Man tänker sig då ofta att man infört nya variabler  u  och  v  som är funktioner av  x  och  y . Med hjälp av kedjeregeln uttrycker man sedan differentialekvationen med hjälp av partiella derivator med avseende på  u  och  v  i stället för med avseende på  x  och  y . Förhoppningen är (här ligger det intelligenta i valet) att denna nya ekvation ska vara lätt att lösa.

Exempel   Lös den partiella differentialekvationen  x²f'_x + y²f'_y = y² genom att införa nya variabler  u = 1/ x - 1/ y och  v = 1/ y.

Kedjeregeln ger

$$\begin{array} {rcl} f'_{x}&=&f'_{u}(-1/x^{2})+f'_{v}\cdot 0\\ f'_{y}&=&f'_{u}(1/y^{2})+f'_{v}(-1/y^{2})\end{array}$$

Ekvationen blir därför  -f'_v = y² = 1/ v² , som ger  f = 1/ v + g(u) = y + g(1/ x - 1/ y),  där  g  är en godtycklig deriverbar funktion.

  

Taylorutveckling

 

Idéen med Taylorutveckling av en funktion  f(t)  runt en punkt  a  är att ersätta  f(t)  med ett polynom  p(t)  i närheten av  a . Polynomet ska väljas så att det har samma derivator som  f  i  a  av ordning upp till och med graden av  p . Ju högre grad man stipulerar för  p  desto bättre approximation av  f  kommer  p  att ge i närheten av  a .

Vi ska försöka genomföra samma typ av idé i fallet där  f  beror på fler än en variabel. Det visar sig att detta följer ganska direkt från envariabelfallet, som vi därför börjar med.

Sats 8   Antag att  f(t)  har kontinuerliga derivator upp till och med ordning  n+1  i en omgivning till  a . Då gäller, i denna omgivning, att

$$f(t)=f(a)+f'(a)(t-a)+\ldots+f^{(n)}(a)\frac{(t-a)^{n}}{n!}+f^{(n+1)}(\theta)\frac{(t-a)^{n+1}}{(n+1)!},$$

där $\theta$ är något tal mellan t och a.

Beviset bygger på en smart partialintegration.

Bevis   Vi har att $f(t)=f(a)+\int_{a}^{t}f'(s)\,ds$. Vi ska använda partiell integration för att integrera integralen. Vi skriver den som $\int_{a}^{t}1\cdot f'(s)\,ds$ och väljer  (s - t)  som primitiv funktion till  1 . Vi får då

$$\begin{array} {rcl} f(t)&=&f(a)+\Big[(s-t)f'(s)\Big]_{a}^{t... ... &=&f(a)+(t-a)f'(a)-\int_{a}^{t}(s-t)f''(s)\,ds.\end{array}$$

Vi fortsätter att integrera partiellt genom att välja  (s - t)²/ 2  som primitiv funktion till  (s - t) . Detta ger

$$\begin{array} {rcl} f(t)&=&f(a)+(t-a)f'(a)-\Big[((s-t)^{2}/... ...{2}f''(a)/2 +\int_{a}^{t}((s-t)^{2}/2)f'''(s)\,ds.\end{array}$$

Upprepar vi nu proceduren  n  gånger får vi

$$\begin{eqnarray*} f(t)&=&f(a)+f'(a)(t-a)+f''(a)(t-a)^{2}/2+\ldots+f^{(n)}(a)(t-... ... & &+(-1)^{n+1}\int_{a}^{t}\frac{(s-t)^{n}}{n!}f^{(n+1)}(s)\,ds. \end{eqnarray*}$$

Funktionen  f^(n + 1)(s)  är kontinuerlig på det slutna intervallet mellan  t  och  a  (om  t  väljs nära  a ) och antar därför ett minsta och största värde där. Kalla dem  m  respektive  M . Vi har då uppskattningen

$$m\int_{a}^{t}\frac{(s-t)^{n}}{n!}\,ds\leq \int_{a}^{t}\frac... ...!}f^{(n+1)}(s)\,ds\leq M\int_{a}^{t}\frac{(s-t)^{n}}{n!}\,ds.$$

eller

$$m\leq \frac{1}{I}\int_{a}^{t}\frac{(s-t)^{n}}{n!}f^{(n+1)}(s)\,ds\leq M,$$

där $I=\int_{a}^{t}(s-t)^{n}/n!\,ds=\Big[(s-t)^{n+1}/(n+1)!\Big]_{a}^{t}=(a-t)^{n+1}/(n+1)!$. Enligt satsen om mellanliggande värden finns ett tal $\theta$ mellan  t  och  a  så att

$$f^{(n+1)}(\theta)=\frac{1}{I}\int_{a}^{t}\frac{(s-t)^{n}}{n!}f^{(n+1)}(s)\,ds,$$

och vi får, efter multiplikation med  (-1)^n + 1I ,

$$(-1)^{n+1}f^{(n+1)}(\theta)\frac{(a-t)^{n+1}}{(n+1)!}=f^{(n+... ...!}=(-1)^{n+1}\int_{a}^{t}\frac{(s-t)^{n}}{n!}f^{(n+1)}(s)\,ds,$$

vilket avslutar beviset.

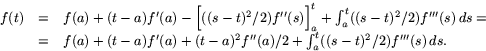
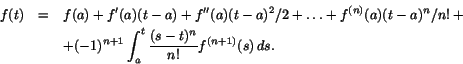
Anmärkning   Det är vanligt att man sätter $B(t)=f^{(n+1)}(\theta)/(n+1)!,$ som är en funktion av  t  eftersom $\theta$ beror på  t . Kontinuiteten av  f^(n + 1)  ger nu att $B(t)\rightarrow f^{(n+1)}(a)/(n+1)!,$ när $t\rightarrow a$. Detta betyder att  B(t)  är begränsad när  t  ligger nära  a .

Polynomet  p_n(t) = f(a) + f'(a)(t-a)+ . . . +f⁽ⁿ⁾(a)(t-a)ⁿ/ n!  kallas Taylorpolynomet till  f  av ordning  n  i punkten  a .

Om man känner till en begränsning på  |f^(n + 1)(t)|  när  t  ligger nära  a  får man ur satsen en uppskattning uppåt av avvikelsen mellan  f  och  p_n . Antag att $\vert f^{(n+1)}(t)\vert\leq K,$ där  K  är en konstant, när $\vert t-a\vert\leq d_{0}$. Vi har då också $\vert f^{(n+1)}(\theta)\vert\leq K,$ och får

$$\vert f(t)-p_{n}(t)\vert\leq K \vert t-a\vert^{n+1}/(n+1)!,$$

när $\vert t-a\vert\leq d_{0}$.

Exempel   Taylorutvecklingen av  f(t) = cos(t)  runt av grad  3  är  p₃(t) = 1 - t²/ 2 . Fjärde derivatan av  f(t) = cos(t)  är  f⁽⁴⁾(t) = cos(t)  som har $\vert f^{(4)}(t)\vert\leq 1$. När $\vert t\vert=\vert t-0\vert\leq d_{0}$ har vi alltså

$$\vert\cos(t)-p_{3}(t)\vert\leq 1\cdot d_{0}^{4}.$$

Om vi beräknar  cos(0.1)  som  p₃(0.1) = 1 - 0.01/ 2 = 0.995  gör vi alltså ett fel som till sin storlek är mindre än  0.1⁴ = 0.0001 .

Vi fortsätter nu med flervariabel fallet. Det återförs på envariabelfallet med ett trick. Vi undersöker bara Taylorutveckling av ordning 2 (linjär approximation) respektive 2 (kvadratisk approximation).

Låt  f  vara en funktion en funktion av  n  variabler och  a  en punkt i $\mathbb{R}^{n}$ med kontinuerliga derivator av ordning  2  respektive  3  i en omgivning till  a . Sätt  g(t) = f(a + t(x-a)) . Vi har då att  g(0) = f(a)  och  g(1) = f(x) . Vi Taylorutvecklar envariabelfunktionen respektive  2 .

Vi har enligt kedjeregeln

$$\begin{eqnarray*} g'(t)=\sum_{i=1}^{n}f_{i}'(\mathbf{a}+t(\mathbf{x}-\mathbf{a})... ...athbf{x}-\mathbf{a})))(x_{i}-a_{i})(x_{j}-a_{j})(x_{k}-a_{k})\\ \end{eqnarray*}$$

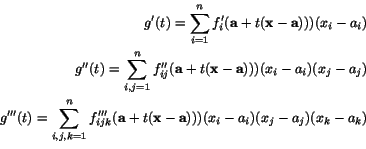
Från envariabelfallet får vi nu

Sats 9   Antag att  f(x)  har kontinuerliga partiella derivator av ordning  2  i omgivning till  a  och att $\vert f_{ij}''(\mathbf{x})\vert\leq M_{L},$ när $\vert\mathbf{x}-\mathbf{a}\vert\leq d_{0}$. Om

$$p_{L}(\mathbf{x})=f(\mathbf{a})+\sum_{i=1}^{n}f'_{i}(\mathbf{a})(x_{i}-a_{i}),$$

så gäller att

$$E_{L}(\mathbf{x})=\vert f(\mathbf{x})-p_{L}(\mathbf{x})\vert\leq \frac{n^{2}}{2}M_{L}\vert\mathbf{x}-\mathbf{a}\vert^{n}.$$

Bevis   Vi har $g(1)=g(0)+g'(0)\cdot 1 +g''(\theta)/2,$ för något $\theta$ mellan och  1 , eller

$$f(\mathbf{x})=f(\mathbf{a})+\sum_{i=1}^{n}f'_{i}(\mathbf{a})(x_{i}-a_{i})+g''(\theta)/2.$$

Uppskattningen av felet är det som återstår. Vi har, med triangelolikheten och förutsättningen

$$\begin{eqnarray*} \vert g''(t)\vert&\leq&\sum_{i,j=1}^{n}\vert f_{ij}''(\mathbf{... ...thbf{a}\vert^{2}=n^{2}M_{L} \vert\mathbf{x}-\mathbf{a}\vert^{2} \end{eqnarray*}$$

Vilket ger

$$E_{L}(\mathbf{x})=\vert g''(\theta)/2\vert=\leq \frac{n^{2}}{2}M_{L} \vert\mathbf{x}-\mathbf{a}\vert^{2}.$$

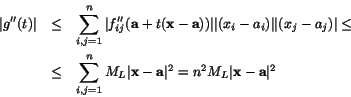
Sats 10   Antag att  f(x)  har kontinuerliga partiella derivator av ordning  3  i omgivning till  a  och att $\vert f_{ijk}'''(\mathbf{x})\vert\leq M_{Q},$ när $\vert\mathbf{x}-\mathbf{a}\vert\leq d_{0}$. Om

$$p_{Q}(\mathbf{x})=f(\mathbf{a})+\sum_{i=1}^{n}f'_{i}(\mathbf... ...sum_{i,j=1}^{n}f''_{ij}(\mathbf{a})(x_{i}-a_{i})(x_{j}-a_{j}),$$

så gäller att

$$E_{Q}(\mathbf{x})=\vert f(\mathbf{x})-p_{Q}(\mathbf{x})\vert\leq \frac{n^{3}}{3!}M_{Q}\vert\mathbf{x}-\mathbf{a}\vert^{n}.$$

Bevis   Vi har $g(1)=g(0)+g'(0)\cdot 1 +g''(0)+g'''(\theta)/3!,$ för något $\theta$ mellan och 1, eller

$$f(\mathbf{x})=f(\mathbf{a})+\sum_{i=1}^{n}f'_{i}(\mathbf{a})... ...}f''_{ij}(\mathbf{a})(x_{i}-a_{i})(x_{j}-a_{j})+g''(\theta)/2.$$

Uppskattningen av felet är det som återstår. Vi har, med triangelolikheten och förutsättningen

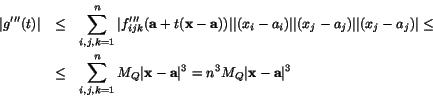
$$\begin{eqnarray*} \vert g'''(t)\vert&\leq&\sum_{i,j,k=1}^{n}\vert f_{ijk}'''(\ma... ...thbf{a}\vert^{3}=n^{3}M_{Q} \vert\mathbf{x}-\mathbf{a}\vert^{3} \end{eqnarray*}$$

Vilket ger

$$E_{Q}(\mathbf{x})=\vert g'''(\theta)/3!\vert=\leq \frac{n^{3}}{3!}M_{Q} \vert\mathbf{x}-\mathbf{a}\vert^{3}.$$