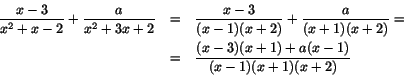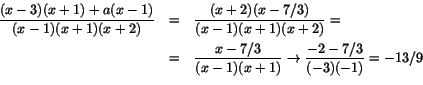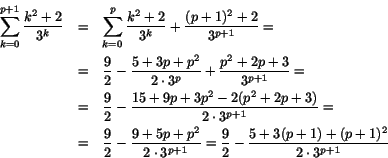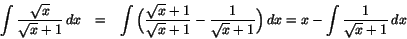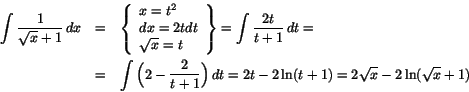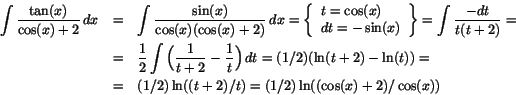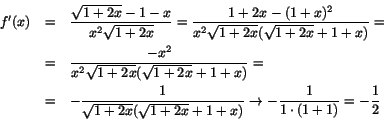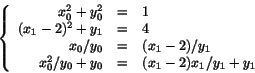Lösningar till TMA 790 Matematisk analys, del A,
02 08 19.
- Vi delar upp i tre fall som bestäms av de ingående
absolutbeloppen.
Fall 1:
 . Ekvationen blir då 3-x=2-3(x+2) eller 2x=-7,
eller x=-7/2 som är
. Ekvationen blir då 3-x=2-3(x+2) eller 2x=-7,
eller x=-7/2 som är 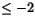 och därför en lösning till den
ursprungliga ekvationen.
Fall 2:
och därför en lösning till den
ursprungliga ekvationen.
Fall 2:
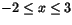 . Ekvationen blir då 3-x=2+3(x+2), eller
-5=4x, eller x=-5/4 som är en lösning till den ursprungliga
ekvationen eftersom
. Ekvationen blir då 3-x=2+3(x+2), eller
-5=4x, eller x=-5/4 som är en lösning till den ursprungliga
ekvationen eftersom
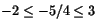 .
Fall 3:
.
Fall 3: 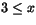 . Ekvationen blir då x-3=2+3(x+2), eller -11=4x,
eller x=-11/4 som inte är
. Ekvationen blir då x-3=2+3(x+2), eller -11=4x,
eller x=-11/4 som inte är 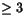 och därför ingen lösning till den
ursprungliga ekvationen.
Svar: x=-5/4 och -7/2.
och därför ingen lösning till den
ursprungliga ekvationen.
Svar: x=-5/4 och -7/2.
- Vi har
Eftersom nämnaren går mot 0 när
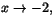 måste även
täljaren göra det för att gränsvärdet ska existera. Täljaren ska
alltså vara 0 när x=-2. Detta ger
0=(-5)(-1)+a(-3), eller
a=5/3.
För täljaren gäller då
måste även
täljaren göra det för att gränsvärdet ska existera. Täljaren ska
alltså vara 0 när x=-2. Detta ger
0=(-5)(-1)+a(-3), eller
a=5/3.
För täljaren gäller då
(x-3)(x+1)+5(x-1)/3=x2-x/3-14/3=(x+2)(x-7/3).
Detta ger
när
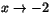 .
Svar: a=5/3. Gränsvärdet blir då -13/9.
.
Svar: a=5/3. Gränsvärdet blir då -13/9.
- Vi visar formeln med induktion. När n=0 är vänstra ledet 2
medan det högra är 9/2-5/2=2. Så formeln stämmer när n=0.
Antag nu att formeln stämmer när n=p. Vi kontrollerar att formeln då
även stämmer när n=p+1. Vänstra ledet är då
Det sista uttrycket är högra ledet när n=p+1. Enligt
induktionsprincipen gäller nu formeln för alla heltal 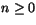 .
.
- Vi har
Vi beräknar den återstående integralen:
- Vi har
Svar: a)
 och b)
och b)
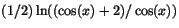 .
.
- För derivata när x=0 ska vi ha att gränsvärdet av uttrycket (f(x)-f(0))/x när
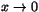 ska existera. Detta uttryck är
ska existera. Detta uttryck är
För att gränsvärdet ska existera måste vi kunna förkorta med
x2. Detta ger oss a=1 och gränsvärdet blir
när
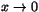 .
För övriga värden på x kan derivatan beräknas med formler. Den blir
.
För övriga värden på x kan derivatan beräknas med formler. Den blir
Vi har alltså
För att avgöra kontinuitet räcker det att undersöka om
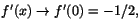 när
när
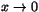 .
Vi har
.
Vi har
så derivatan är kontinuerlig när x>-1/2.
- Från en figur (eller genom implicit derivering) ser vi att
tangentlinjen till en punkt (x0,y0) på den första cirkeln har
riktningskoefficient -x0/y0 medan tangentlinjen till en
punkt (x1,y1) på den andra har riktningskoefficient
-(x1-2)/y1.
Tangentlinjens ekvation genom de två punkterna är därför
y=-(x0/y0)(x-x0)+y0 respektive
y=-((x1-2)/y0)(x-x1)+y1. Vi söker de två punkterna så
att dessa ekvationer bestämmer samma linje. Vi ska då ha
x0/y0=(x1-2)/y1 och
x02/y0+y0=(x1-2)x1/y1+y1. För att bestämma
de två punkterna ska vi alltså lösa ekvationssystemet
Vänstra ledet i den sista ekvationen kan skrivas
(x02+y02)/y0=1/y0 medan det högra kan skrivas
((x1-2)x1+y12)/y1=((x1-2)2+y12+2x1-4)/y1=2x1/y1
Detta ger oss
y0=y1/(2x1), som i tredje ekvationen ger
x0=(x1-2)/(2x1), som insatt i den första ger
(x1-2)2+y12=4x12. Tillsammans med den andra ger
detta 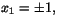 där -1 är uteslutet. Vi har alltså x1=1,
som i cirkelns ekvation ger
där -1 är uteslutet. Vi har alltså x1=1,
som i cirkelns ekvation ger
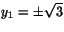 där
där 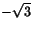 ger
riktningskoefficient <0 och därför är uteslutet. Tangentlinjens
ekvation blir därför:
ger
riktningskoefficient <0 och därför är uteslutet. Tangentlinjens
ekvation blir därför:
Svar:

Jan-Alve Svensson
2002-08-21