Lösningar till Matematisk analys I, TMA790, del c, 02 08 29.
- Triangelytan är sluten och begränsad och funktionen är kontinuerlig, så den antar säkert ett största och ett minsta värde i ytan.
Vi söker först stationära punkter i det inre av ytan genom att lösa ekvationssystemet

Från den första ekvationen har vi y=0 eller y=4-2x. I den andra ekvationen ger detta x godtyckligt respektive x(4-2x)(4x-4), dvs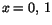 eller 2. Systemets lösningar är (x,0), där x är godtycklig, (0,4), (1,2) samt (2,0. Av dessa är endast (1,2) en inre punkt i ytan. Vi har f(1,2)=4.
Vi undersöker f längs ytans rand:
1) f(t,0)=0, där
eller 2. Systemets lösningar är (x,0), där x är godtycklig, (0,4), (1,2) samt (2,0. Av dessa är endast (1,2) en inre punkt i ytan. Vi har f(1,2)=4.
Vi undersöker f längs ytans rand:
1) f(t,0)=0, där 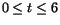 2) f(0,t)=0, där
2) f(0,t)=0, där 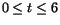 3)
f(6-t,t)=t2(4(6-t)-(6-t)2-(6-t)t)=2t3-12t2, där
3)
f(6-t,t)=t2(4(6-t)-(6-t)2-(6-t)t)=2t3-12t2, där 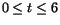 .
Derivatan av detta är 0 när t=0, eller 4. Vi har
f(6,0)=0=f(0,6) och f(2,4)=-64.
.
Derivatan av detta är 0 när t=0, eller 4. Vi har
f(6,0)=0=f(0,6) och f(2,4)=-64.
Svar: 4 respektive -64. - Kedjeregeln ger
f'x=f'u2ax+f'v och f'y=f'u. Väljer vi a=1/2 blir ekvationen
f'v=y=u-v2/2, som ger
f=uv-v3/6+g(u), där g(u) är en godtycklig deriverbar funktion. Vi har alltså att lösningarna ges av
f(x,y)=(x2/2+y)x-x3/6+g(x2/2+y)=x3/3+yx+g(x2/2+y).
Vi söker g så att
x2+x3/3=f(x,0)=x3/3+g(x2/2). Detta ger g(x2/2)=x2 eller g(t)=2t. Den speciella lösnigen är allstå
f(x,y)=x3/3+yx+x2+2y.
Svar: f(x,y)= x3/3+yx+g(x2/2+y), där g är en godtycklig deriverbar funktion, respektive f(x,y)=x3/3+yx+x2+2y. - Triangelytan ges av olikheterna
 och
och 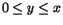 . Vi får därför
. Vi får därför
![\begin{eqnarray*}
\int\!\int_D(x^2+y^2)\,dxdy&=&\int_0^1\Big[x^2y+y^3/3\Big]_0^x\,dx=\\
&=&\int_0^1 4x^3/3\,dx=\Big[x^4/3\Big]_0^1=1/3.
\end{eqnarray*}](img6.gif)
Svar: 1/3. - Enligt Greens formel blir kurvintegralen
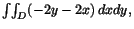 där D begränsas av de två kurvorna. Deras skärningspunkt ges av ekvationssystemet
där D begränsas av de två kurvorna. Deras skärningspunkt ges av ekvationssystemet
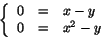
dvs av (0,0) och (1,1). Området D ges därför av och
och
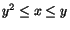 . Därför får vi
. Därför får vi
![\begin{eqnarray*}
\int\!\int_D (-2y-2x)\,dxdy&=&\int_0^1\Big[-2xy-x^2\Big]_{y^2...
...\, dy=\Big[-y^3+y^4/2+y^5/5\Big]_0^1=\\
&=&-1+1/2+1/5=-3/10.
\end{eqnarray*}](img11.gif)
Svar: -3/10. - I skärningen mellan de två ytorna gäller att 4x=x2+y2 dvs 4=(x-2)2+y2.
Det betyder att K är instängd mellan grafen till x2+y2 och 4x ovanför cirkeln
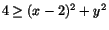 i xy-planet.
Vi ska beräkna
i xy-planet.
Vi ska beräkna
 som alltså blir
som alltså blir
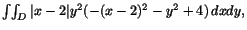 där D ges av
där D ges av
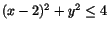 . Övergång till polära koordinater,
. Övergång till polära koordinater,
 ger oss
ger oss
 där D' ges av
där D' ges av  och
och
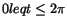 .
Vi får
.
Vi får
![\begin{eqnarray*}
\int\!\int_{D'}r\vert\cos(t)\vert r^2\sin^2 t(4-r^2)\,drd\the...
..., dt=\\
&=&(2^8/35)4\Big[\sin^3 t/3\Big]_0^{\pi/2}=1024/105.
\end{eqnarray*}](img20.gif)
Svar: 1024/105. - Integranden är kontinuerlig ut till randen av D, så vi kan utgå från att D ges av
 och
och  .
Vi väljer en uttömmande följd av kompakter Dk till D genom att låt Dk definieras av
.
Vi väljer en uttömmande följd av kompakter Dk till D genom att låt Dk definieras av
 och
och
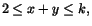 där k är ett heltal >2.
I dubbelintegralen
där k är ett heltal >2.
I dubbelintegralen
 gör vi variabelsybstitutionen u=x-y och v=x+y. Vi har
d(u,v)/d(x,y)=2, och Dk motsvaras av Dk' som ges av
gör vi variabelsybstitutionen u=x-y och v=x+y. Vi har
d(u,v)/d(x,y)=2, och Dk motsvaras av Dk' som ges av
 och
och 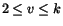 . Vi får
. Vi får
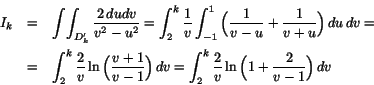
Integranden är positiv ( ), så följden Ik är växande. För att visa att den konvergerar (och därmed visa att den ursprungliga integralen är konvergent) räcker det att visa att den är uppåt begränad. Vi har (den kända) olikheten
), så följden Ik är växande. För att visa att den konvergerar (och därmed visa att den ursprungliga integralen är konvergent) räcker det att visa att den är uppåt begränad. Vi har (den kända) olikheten
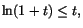 när
när 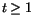 . Vi får därför
. Vi får därför
![\begin{eqnarray*}
I_k&\leq&\int_2^k\frac{2}{v}\cdot\frac{2}{v-1}\,dv=4\int_2^k\...
...&4\Big[\ln((v-1)/v)]_2^k=4(\ln(1-1/k)+\ln 2)\rightarrow 4\ln 2,
\end{eqnarray*}](img31.gif)
när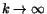 . Detta ger att följden Ik är uppåt begränsad.
. Detta ger att följden Ik är uppåt begränsad.
Svar: Integralen är konvergent.
Jan-Alve Svensson
2002-08-29