Rätt! Om det funnes en sådan triangel skulle vi ha att 3² = 2² + 2² men detta stämmer ju inte. Alltså kan det inte finnas någon sådan triangel.

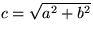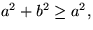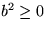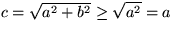Om hypotenusan har längd c och de båda katetrarnana har längd a respektive b, så gäller att enligt Pythagoras sats. Men eftersom . Detta ger . Genomför samma argument för att 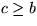som övning!

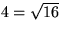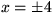Rätt! Av beteckningarna framgår att c är katetern, så vi måste ha 5² = 3² + b² . Subbtraherar man 3² = 9 i båda leden får man 16 = b², eller b = 4 eftersom . Observera att ekvationen 16 = x² egentligen har två lösningar: . Men vi vet ju att b är längden av en sida och därför positiv, så b = 4 .

Något har blivit fel. Av beteckningarna i uppgiften framgår att c är katetern, så Pythagoras sats ger 5² = 3² + b² . Vad är b ? Rätt! Det finns faktiskt två svar på frågan och detta beror på att katetern kan finnas bland de kända sidorna eller vara den okända sidan.

Om katetern är en av de kända sidorna har den längd 5 eftersom hypotenusan är den längsta sidan. Pythagoras sats ger 5² = a² + 4², där a är den okända längden av en av katetrarna. Detta ger a = 3 .

Om hypotenusan betecknas c och är okänd ger Pythagoras sats att c² = 4² + 5² eller .

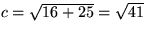Observera att svaret beror på om hypotenusans längd är en av de kända längderna eller inte.

Svara på följande vis: x eller y, där x och y är dinna svar och x är minst. Kvadratrötter ska skrivas: sqrt(x), t.ex skrivs 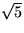som sqrt(5).

Rätt svar! Men hur i allsin dar visste Du det! Satte Du in värden i formeln i Pythagoras sats och såg att det stämde? I såfall lyckades Du bara inse att det inte är omöjligt att det finns en sådan triangel. Klicka på hjälpknappen för en förklaring!

Ditt svar var fel, men det kanske inte var så tokigt ändå! Klicka på hjälpknappen för en förklaring.

Observera att Pythagoras sats säger att om man vet att ACB är en rätvinklig triangel, så vet man också att c² = a² + b² . Satsen säger inte att om man vet att c² = a² + b² , så är ACB vinkelrät. Detta är visserligen sant och brukar kallas omvädningen till Pythagoras sats. En sats som kallas cosinussatsen är en mycket mer allmän sats säger att om ACB är en triangel (alltså inte nödvändigtvis rätvinklig) och 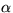är vinkeln vid C, så gäller att . 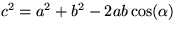Om vi nu sätter 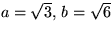får vi 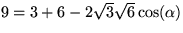och därfö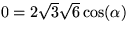r . Men om en produkt av tal är 0 , så måste en av faktorerna vara 0 . Den enda möjligheten är 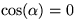som i sin bara har lösningen 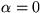(eftersom 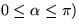. Rätt!

Försök igen! Primtalen som är < 5 är 2, 3 och 5.

Rätt!

Försök igen!

Rätt!

Försök igen! Primtalen som är < 11 är 2, 3, 5, 7, och 11.

Nästa steg

Visa igen

Föregående steg

Det är riktigt att summan av de markerade vinklarna vid A är 180 °. Men det vikitga är att vinklarna 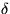och 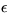är två av triangelns vinklar. Vilka?

Det är riktigt att det finns två parallella linjer i figuren, men det viktiga är att vinklarna 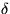och 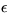är två av triangelns vinklar. Vilka?

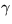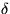Det stämmer att triangeln ABC delas upp i två trianglar med medelpunkt i O. Men det väsentliga är att dessa är likbenta. Det gör att man kan säga något om och . Vad?

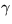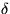Det stämmer att trianglarna AOC och OBC har samma area. De har ju samma bas (radien i cirkeln) och samma höjd. Men det är inte så lätt att utnyttja detta för att förstå att vinkeln vid C är rät. Lägg istället märke till att de två trianglarna är likbenta. Detta ger något om vinklarna och . Vad?

Summan av de fyra vinklarna är 180°, eftersom vinkelsumman i en triangel är 180°.

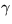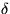Utnyttja nu att och kan uttryckas med de övriga två markerade vinklarna. Den ena stora kvadraten har sida 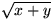medan den lilla har sida 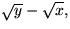om vi förutsätter att y är större än eller lika med x . Men det verkar svårt att untyttja detta till något vettigt.

Trianglarna har tillsammans arean 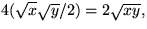medan den lilla kvadraten har area 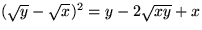. Väljer man nu t.ex. x = 1 / 4 och y = 4 har trianglarna sammanlagd area 2, medan den lilla kvadraten har area 2 + 1 / 4 . Påståendet stämmer alltså inte i alla tillfällen.

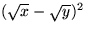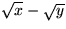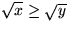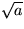Om man drar roten ur får man inte i allmänhet. Det stämmer bara om . Förklaringen till detta är att en kvadratrot alltid är större än eller lika med 0. Kvadratroten kan alltså inte vara negativ. Om 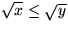är istället roten ur 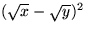lika med !

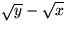Det verkar svårt att utnyttja detta till att förstå något om förhållandet mellan 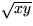och ( x + y ) / 2 .

Konjugatregeln säger att a² - b² är lika med produkten ( a - b )( a + b ).

Uttrycket 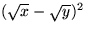kan inte skrivas om med denna räkneregel! Felaktig formel!