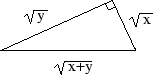En av de mest välkända matematiska satserna bland allmänheten är
Pythagoras sats från antiken:
Sats:
Om ACB är en rätvinklig triangel, så är
c2 = a2 + b2 .
Denna koncisa formulering av satsen bygger på att man är bekant med
matematiskt språkbruk och betäckningssätt. Låt oss titta närmare på
hur detta fungerar!
När man skriver att ABC är en triangel i planet, betyder det att man
har tre punkter i planet som betecknas
 respektive C. Den
triangel det är fråga om när man skriver triangeln ABC är den
man får genom att förena de tre punkterna med varandra parvis med
streckor:
respektive C. Den
triangel det är fråga om när man skriver triangeln ABC är den
man får genom att förena de tre punkterna med varandra parvis med
streckor:
När man säger att ACB är en rätvinklig triangel betyder det att
vinkeln vid C (den mittersta punkten i uppräkningen ACB) är
rät. För att markera att vinkeln vid C är rät brukar man sätta en
liten kvadrat vid detta hörn som i figuren nedan.
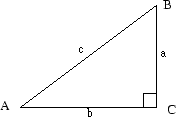
Givet dessa beteckningar betyder c längden av den mot
C stående sidan i triangeln (d.v.s den sida, eller
strecka, som inte råkar C ). På samma sätt betecknar a
och b längden av de mot A respektive B stående
sidorna:
Den sida som står mot det vinkelräta hörnet kallas hypotenusa,
medan de andra två är katetrar i den rätvinkliga
triangeln. Hypotenusans längd, med våra beteckningar c, är alltid
längre än katetrarnas längder, i vårat fall a respektive b.
Innebörden i Pythagoras sats är att i en rätvinklig triangel ACB
gäller ett visst samband mellan de tre talen
 och c, nämligen
och c, nämligen
c2 = a2 + b2
Detta samband betyder t.ex. att om man känner till vad a och
b är, så kan man beräkna c, som
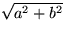 .
Men formeln ger också att om man känner till a och c så
kan man beräkna b. Om vi i nämligen subbtraherar
a2 i de båda leden i formeln, får vi
c2-a2 = b2 och
sedan
.
Men formeln ger också att om man känner till a och c så
kan man beräkna b. Om vi i nämligen subbtraherar
a2 i de båda leden i formeln, får vi
c2-a2 = b2 och
sedan
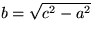 .
Den allmänna slutsatsen av Pythagoras sats är att om man i en
rätvinklig triangel känner längderna av två av sidorna så kan man
beräkna den tredje.
Låt oss se om Du förstår innebörden av Pythagoras sats. Fundera över
följande frågor:
.
Den allmänna slutsatsen av Pythagoras sats är att om man i en
rätvinklig triangel känner längderna av två av sidorna så kan man
beräkna den tredje.
Låt oss se om Du förstår innebörden av Pythagoras sats. Fundera över
följande frågor:
Testövning 1.1
a) Finns det någon rätvinklig triangel med sidor vars längder är 2 ,
2 , respektive 3 ?
 Ja
Ja
 Nej
Nej
b)
Varför är har hypotenusan större längd en var och en av katetrarna i
en rätvinklig triangel?
 Hjälp
Hjälp
c)
I den rätvinkliga triangeln ACB är a = 3 och
c = 5 . Vad är b ?
d)
I en rätvinklig triangel har två av
sidorna längd 4 respektive 5 . Vilken längd har den tredje sidan?
e) I triangeln ACB har sidorna längd
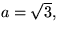
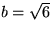 och c = 3. Är ACB rätvinklig?
och c = 3. Är ACB rätvinklig?
 Ja
Ja
 Nej
Nej
 Hjälp
Hjälp
I matematiken vimlar det av olika påståenden. T.ex.
- Om x > 1 så är 2x > 2 ,
- 5 är inte delbart med 3 ,
- Varje heltal mindre än 100 , är det delbart med ett heltal mellan
2 och 10 ,
- Om en cirkel har radie r , så har den omkrets
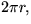
- Om ABC är en triangel, så är summan av dess vinklar 180
° (eller
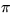 ).
).
En del påståenden stämmer, andra inte (de är sanna (korrekta)
eller falska (felaktiga))). Exempelvis stämmer inte
påståendet ''Varje heltal mindre än 100 , är delbart med ett heltal
mellan 2 och 10 ,'' för om man väljer 31 så är det mindre än 100, men
inte delbart med något heltal mellan 2 och 3 .
En del sanna påståenden är så betydelsefulla att de förtjänar att
kallas satser. Oftast är det heller inte lätt att omedelbart
förstå att de är korrekta; det krävs ett bevis för
detta.
Påståendet ''om x > 1 så är 2x > 2,'' är visserligen
sant, men inte så betydelsefullt för matematik i allmänhet att det
förtjänar att kallas en sats. Däremot kan det vara viktigt i en
speciell situation.
Gemensamt för de flesta satserna (och påståenden) är att de består av
två delar:
- en (rad) förutsättning(ar),
- en slutsats (som påstås stämma om förutsättningarna gäller).
Även om satser i allmänhet har denna form är den inte alltid så
uppenbart formulerad. Man får komma ihåg att språkbruket i matematik
har utvecklats av människor för människor!
I Pythagoras sats så är förutsättningen att ACB är en
rätvinklig triangel och slutsatsen är att
c2 = a2 + b2.
I (det felaktiga) påståendet ''Varje heltal mindre än 100, är det
delbart med ett heltal mellan 2 och 10 ,'' är den delvis outtalade
förutsättnignen att man har ett heltal mindre än 100 och slutsatsen är
att det (i så fall) är delbart med något av talen
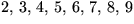 eller 10 .
eller 10 .
Det är viktigt att hålla isär förutsättningar och slutsats; om man
t.ex. har en triangel ABC med sidor av längd
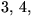 och 5, så är 52 = 32 + 42 . Slutsatsen i
Pythagoras sats stämmer alltså, men av det kan man inte, med hjälp av
Pythagoras sats, dra slutsatsen att ABC är en rätvinklig
triangel. Detta är visserligen korrekt, men man kan inte förstå det
genom att använda Pythgaoras berömda sats.
och 5, så är 52 = 32 + 42 . Slutsatsen i
Pythagoras sats stämmer alltså, men av det kan man inte, med hjälp av
Pythagoras sats, dra slutsatsen att ABC är en rätvinklig
triangel. Detta är visserligen korrekt, men man kan inte förstå det
genom att använda Pythgaoras berömda sats.
Låt oss nu se om vi kan bevisa Pythagoras sats.
Syftet med ett bevis är att ställa det utom allt tvivel, för en själv
och andra, att satsen är korrekt. När en sats väl bevisats kan den
användas utan att man vid varje enskilt tillfälle behöver förstå
varför den är sann.
I ett bevis kan man använda sig av
- satsens förutsättningar,
- redan kända (bevisade) satser och förhållanden,
- fiffiga knep,
- och ett logiskt korrekt resonemang.
Den första punkten avslöjar genast att det som en person uppfattar som
ett bevis, inte behöver vara ett bevis för en annan; det kan krävas en
rad förkunskaper för att förstå varför ett bevis är just ett bevis. Om
något är ett bevis eller inte är alltså inte helt glasklart!
Den tredje punkten avslöjar varför det kan vara svårt att bevisa ett
påstående; förmågan att finna de finurliga trixen bygger på lång
erfarenhet av matematik, men är något man kan lära sig med tiden! Här
finns också en skönhetsaspekt! Ett bevis för en sats kan bestå av en
mängd (i bland oöverskådliga) knep, medan ett annat bevis för samma
sats kan kan nöja sig med ett (enda genialt) knep.
Man kan undra om man inte kan ''bevisa'' en sats genom att helt enkelt
pröva den i en lång rad fall och se att slutsatsen är korrekt. Här är
ett varnande exempel:
Sats: Om n är ett heltal > 1 och m är produkten
av alla primtal mellan 2 och n, så är m + 1 ett primtal.
Mins att ett heltal
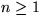 är ett primtal om det bara har det inte kan skrivas som produkt av två
heltal > 1. T.ex. är 3, 2, 5, 7, 11, 13, 19 och 23 primtal, men
också 2311 (vilket inte är så uppenbart!).
är ett primtal om det bara har det inte kan skrivas som produkt av två
heltal > 1. T.ex. är 3, 2, 5, 7, 11, 13, 19 och 23 primtal, men
också 2311 (vilket inte är så uppenbart!).
Man kan, och det är vettigt att göra detta, pröva och se om satsen
gäller för några värden pä n = 2
Om n = 2, så är
m = 2 och m + 1 = 3 , som ju är ett primtal. Slutsatsen stämmer
alltså i detta fall.
Om n = 3 , så är
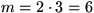 och m + 1 = 7 . Slutsatsen stämmer även i detta fall!
och m + 1 = 7 . Slutsatsen stämmer även i detta fall!
Om
n = 4 , så är
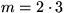 och m + 1 = 7 , så slutsatsen stämmer.
och m + 1 = 7 , så slutsatsen stämmer.
Testövning 1.2
Vad är m + 1 om
a) n = 5 ?
b) n = 7 ?
c) n = 11 ?
När n = 13 är
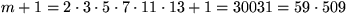 som alltså inte är ett primtal. Alltså är slutsatsen i satsen
felaktig. Satsen är med andra ord ingen riktig sats utan
felaktig. (Lägg den därför inte på minnet!)
som alltså inte är ett primtal. Alltså är slutsatsen i satsen
felaktig. Satsen är med andra ord ingen riktig sats utan
felaktig. (Lägg den därför inte på minnet!)
Vi ser att man kan hålla på ett bra tag att testa en sats praktiskt
utan att för den skull lyckas komma fram till att den är korrekt. Vi
hade tur som bara behövde hålla på till n = 13 för att inse att
satsen var felaktig.
Vi härmed högtidligen och för all framtid, förkasta det praktiska
testandet i ett antal fall som metod att bevisa påståenden i
matematik.
Här följer nu ett bevis för Pythagoras sats. Starta genom att klicka
på knappen:
 Starta beviset
Starta beviset
Börja med att rita en kvadrat med sida samma längd som hypotenusan i
triangeln.
Lägg sedan in triangeln som i figuren. Eftersom vinkelsumman i en
triangel är 180° (redan känt förhållande) och vinkeln vid
C är 90° enligt förutsättningen, är
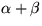 lika med 90° . Detta ger att
lika med 90° . Detta ger att
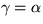 .
.
Vi kan därför lägga in triangeln ytterligare en gång i kvadraten som i
figuren.
Proceduren kan upprepas en gång till enligt samma argument som
tidigare.
En sista upprepning ger resultatet i figuren. Med hjälp av det
knep vi nu genomfört kan vi ganska lätt komma fram till
slutsatsen i Pytagoras sats genom att jämföra areor (använder
tidigare kända begrepp).
Observera att det i figuren uppstått en liten kvadrat inuti den stora
vars sida har längd b - a. Därför har den area
( b - a )2. Om vi beräknar den större kvadratens
area genom att summera trianglarnas areor och den mindre kvadratens
area får vi
c2 = 4( ab / 2 ) + ( b - a )2
Utveckling av högra ledet ger
2ab + ( b2 - 2ab +
a2) =
b2 + a2 och därför har vi fått
c2 = a2 + b2
och beviset för Pythagoras sats är klart!
Nu ska du fä chansen att pröva på att göra egna bevis. Du får lite
hjälp med de knep som är nödvändiga. Klicka på ett alternativ för att
starta.
 Vinkelsumman i en triangel
Vinkelsumman i en triangel
 Rätvinkliga trianglar
Rätvinkliga trianglar
 En välkänd olikhet
En välkänd olikhet
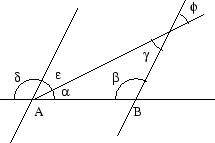
Sats: Summan av vinklarna i en triangel är 180°
(eller
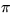 ).
).
Låt ABC vara en triangel vilken som helst. Låt oss rita en figur:
Det är nu viktigt att försöka förstå att även om vi ritat en alldeles
speciell triangel, så kommer det vi gör i fortsättningen att funger
för vilken triangel som helst.
Drag linjen genom A och B och drag en linje genom
A som är parallell med streckan BC:
Varför kan detta vara ett användbart knep?
 Man känner igen
vinklarna vid A.
Man känner igen
vinklarna vid A.
 Summan av de markerade
vinklarna vid A är 180° .
Summan av de markerade
vinklarna vid A är 180° .
 Eftersom det
finns två parallella linjer i figuren, måste summan av tre
vinklar bli 180° .
Eftersom det
finns två parallella linjer i figuren, måste summan av tre
vinklar bli 180° .
Vi ser att
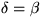 att
att
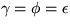 och att
och att
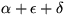 är 180° . Tillsammans ger detta att
är 180° . Tillsammans ger detta att
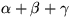 är 180° .
är 180° .
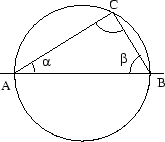
Sats: Om AB är diagonal till en cirkel och C är
en annan punkt på denna cirkel, så har triangeln ABC rät vinkel vid
C
Låt oss rita en figur för att förstå hur det hela ser ut:
Det är viktigt att du i beviset inte använder att C valts på ett
speciellt sätt.
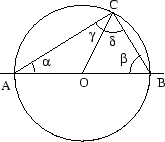
Markera mittpunkten på streckan AB och kalla den O. Drag också
streckan OC:
Varför är detta knep användbart?
 Triangeln ABC
delas upp i två trianglar som har ett hörn i cirkelns
medelpunkt.
Triangeln ABC
delas upp i två trianglar som har ett hörn i cirkelns
medelpunkt.
 Triangeln ABC
delas upp i två likbenta trianglar.
Triangeln ABC
delas upp i två likbenta trianglar.
 Trianglarna
AOC och BCO har samma area.
Trianglarna
AOC och BCO har samma area.
Eftersom AOC är likbent måste
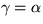 och
och
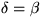 .
Vinkelsumman i en triangel är 180° och vinkeln vid C är
.
Vinkelsumman i en triangel är 180° och vinkeln vid C är
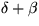 .
.
Vad är nu
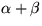 ?
?
Sats: Om x och y är positiva rella tal, så gäller
att
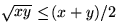 .
.
Här får du möjlighet att välja mellan två typer av bevis
 Ett geometriskt
bevis.
Ett geometriskt
bevis.
 Ett algebraiskt
bevis.
Ett algebraiskt
bevis.
Börja med att rita en rätvinklig triangel med katetrar av längd
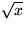 respektive
respektive
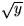 :
:
Enligt Pythagoras sats har hypotenusan längd
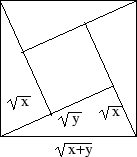
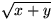 Lägg in triangeln fyra gånger i kvadraten med
sida
Lägg in triangeln fyra gånger i kvadraten med
sida
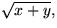 som i beviset för Pythagoras sats:
som i beviset för Pythagoras sats:
Varför är detta en fiffig konstruktion?
 Man kan
jämföra längder i de två kvadrater som uppstått.
Man kan
jämföra längder i de två kvadrater som uppstått.
 Man kan
jämföra areor.
Man kan
jämföra areor.
 Summan av
trianglarnas area är större än den lilla kvadratens area
Summan av
trianglarnas area är större än den lilla kvadratens area
Den stora kvadratens area är
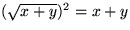 medan summan av trianglarnas area är
medan summan av trianglarnas area är
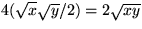 som är mindre än (eller lika med) kvadratens area, d.v.s.
som är mindre än (eller lika med) kvadratens area, d.v.s.
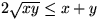 .
Division med 2 på båda sidor ger nu
.
Division med 2 på båda sidor ger nu
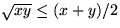
Eftersom en kvadrat allltid är större än eller lika med 0, har man
att
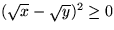 .
.
Varför kan detta vara användbart?
 Om man drar
roten ur båda leden får man något användbart.
Om man drar
roten ur båda leden får man något användbart.
 Utveckling
ger något användbart.
Utveckling
ger något användbart.
 Man kan
använda konjugatregeln för att se något användbart.
Man kan
använda konjugatregeln för att se något användbart.
Utveckling ger
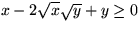 och addition av
och addition av
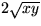 i båda leden ger sedan
i båda leden ger sedan
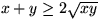 .
Division med 2 i båda leden ger nu
.
Division med 2 i båda leden ger nu
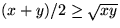 .
.
![]() respektive C. Den
triangel det är fråga om när man skriver triangeln ABC är den
man får genom att förena de tre punkterna med varandra parvis med
streckor:
respektive C. Den
triangel det är fråga om när man skriver triangeln ABC är den
man får genom att förena de tre punkterna med varandra parvis med
streckor: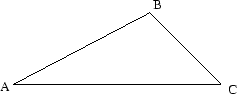
![]() och c, nämligen
och c, nämligen
![]() Ja
Ja
![]() Nej
Nej ![]() Hjälp
Hjälp ![]()
![]() och c = 3. Är ACB rätvinklig?
och c = 3. Är ACB rätvinklig?