Avståndet mellan två tal x och y på tallinjen betecknas
| y - x |.
Om x ligger till vänster om y ( x < y ) är
| y - x | = y - x, men om x ligger till
höger om y ( x > y ), så är
| y - x | = -( y - x ) = x - y.
Speciellt ges avståndet mellan 0 och x av | x |. Om
x > 0 är | x | = x, men om x < 0 är
| x | = -x.
Eftersom x och -x har samma avstånd till 0 som -x har vi att
| x | = | -x |.
Detta ger att
| y - x | = | -(y - x) | = | x -
y |.
Testövning 2.1 Vad är avståndet mellan
x och y om
Exempel 2.1 För vilka tal
x
gäller att |
x -1 | < 2?
Det gäller alltså att bestämma för vilka värden på x som avståndet
mellan x och 1 är mindre än 2. De tal som befinner sig på
avstånd mindre än 2 från talet 1 är de som ligger mellan 1 - 2 = -1 och
1+2=3. Svaret blir alltså: det tal x sådana att -1 <
x < 2.
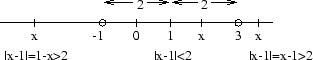
Exempel 2.2 För vilka tal x
gäller att | x - 1 | + | x + 3 | < 5 ?
Hur lyder tolkningen av uppgiften med hjälp av avståndsbegreppet?
 Man söker de tal x sådana att avstånden till 1 och 3
samtidigt är mindre än eller lika med 5.
Man söker de tal x sådana att avstånden till 1 och 3
samtidigt är mindre än eller lika med 5.
 Man söker de tal x sådana att summan av avstånden
mellan x och 1 och x och 3 är mindre än eller lika med
5.
Man söker de tal x sådana att summan av avstånden
mellan x och 1 och x och 3 är mindre än eller lika med
5.
 Man söker de tal x sådana att summan av avstånden mellan
x och 1 och x och -3 är mindre än eller lika med
5.
Man söker de tal x sådana att summan av avstånden mellan
x och 1 och x och -3 är mindre än eller lika med
5.
Svaret blir alltså alla tal x sådana att
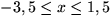 .
.
Exempel 2.3 För vilka tal x
gäller att | x - 4 | = 3 + | x + 2 | ?
Hur lyder tolkningen av uppgiften med hjälp av avståndsbegreppet?
 Avståndet mellan x och 4 ska var lika med summan av 3 och avståndet
mellan x och 2.
Avståndet mellan x och 4 ska var lika med summan av 3 och avståndet
mellan x och 2.
 Förenklingen 3 + 2 = 5 ger att tolkningen blir: avståndet mellan
x och 4 ska vara lika med avståndet mellan x och - 5 .
Förenklingen 3 + 2 = 5 ger att tolkningen blir: avståndet mellan
x och 4 ska vara lika med avståndet mellan x och - 5 .
 Avståndet mellan x och 4 ska vara lika med summan av 3 och avståndet
mellan x och - 2 .
Avståndet mellan x och 4 ska vara lika med summan av 3 och avståndet
mellan x och - 2 .
Vi ska alltså bestämma alla tal x sådana att avståndet mellan x
och 4 är 3 (längdenheter) större än avståndet mellan x och -2.
Svaret blir alltså x=-0,5.
Grafen till funktionen x2 ser ut så här:
 Visa
Visa
För att lösa ekvationen x2 = a (där a är
känt) ska man bestämma x - koordinaten för skärningspunkterna
mellan grafen och linjen y = a (linje parallell med
x-axeln genom punkten ( 0, a) ).
Om a < 0
finns ingen lösning till x2 = a eftersom en
kvadrat alltid är icke-negativ
 Visa
Visa
Om a = 0 har ekvationen bara lösningen x = 0 .
 Visa
Visa
Om a > 0 finns det precis två olika lösningar till
x2 = a ; en positiv och en negativ. Den positiva
lösningen kallas kvadratroten ur a och betecknas
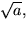 så att
så att
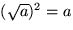 .
Eftersom
.
Eftersom
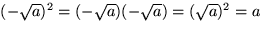 och
och
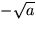 är negativt är
är negativt är
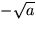 den andra lösningen.
den andra lösningen.
 Visa
Visa
Observera att om man använder beteckningen
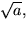 så förutsätter man att a är icke-negativt; annars är symbolen
meningslös.
så förutsätter man att a är icke-negativt; annars är symbolen
meningslös.
Talet
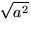 är den icke-negativa lösningen till
x2 = a2 . Ekvationen har precis två
lösningar om
är den icke-negativa lösningen till
x2 = a2 . Ekvationen har precis två
lösningar om
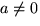 och dessa är
och dessa är
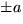 .
Om a > 0 är a den positiva av dessa lösningar, men
om a < 0 är -a den postiva. Det gäller alltså att
.
Om a > 0 är a den positiva av dessa lösningar, men
om a < 0 är -a den postiva. Det gäller alltså att
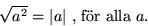
Eftersom
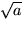 löser ekvationen x2 = a har vi
löser ekvationen x2 = a har vi
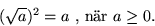
Ekvationen x2 = ab har den positiva lösningen
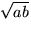 när ab > 0. Om
när ab > 0. Om
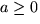 och
och
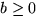 är
är
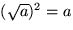 och
och
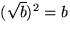 och
och
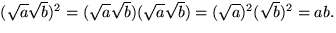 Vi ser att
Vi ser att
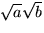 är en lösning till x2=ab, som är positiv
eftersom produkten av två positiva tal är positiv. Vi har alltså
är en lösning till x2=ab, som är positiv
eftersom produkten av två positiva tal är positiv. Vi har alltså
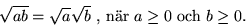
Det går inte att hitta en motsvarande formel för
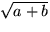 .
Det är mycket populärt, men tyvärr felaktigt
att använda formeln
.
Det är mycket populärt, men tyvärr felaktigt
att använda formeln
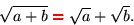
Om man t.ex. väljer a=b=1 ger denna ``formel'' det felaktiga
resultatet

Vi vet att
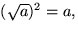 när
när
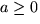 .
Om a > 0 kan vi invertera de båda leden och får då
.
Om a > 0 kan vi invertera de båda leden och får då
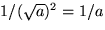 .
Nu är
.
Nu är
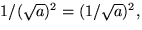 så vi ser att
så vi ser att
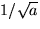 (som är positivt) löser ekvationen x2=1/a
vars positiva lösning är
(som är positivt) löser ekvationen x2=1/a
vars positiva lösning är
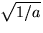 .
Vi har alltså
.
Vi har alltså
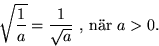
Exempel 2.5 Skriv
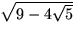 med högst ett rottecken.
med högst ett rottecken.
Exempel 2.6 Skriv
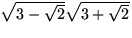 med högst ett rottecken.
med högst ett rottecken.
Hur tycker du man ska börja?
 Skriva om de två faktorerna som
Skriva om de två faktorerna som
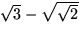 respektive
respektive
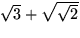 och använda konjugatregeln.
och använda konjugatregeln.
 Skriva de yttersta kvadratrötterna som en enda.
Skriva de yttersta kvadratrötterna som en enda.
 Kvadrera allt ihopa så att de yttre rötterna försvinner och sedan
multiplicera samman.
Kvadrera allt ihopa så att de yttre rötterna försvinner och sedan
multiplicera samman.
Det kan vara lämpligt att göra omskrivningen
 =
=
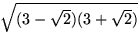
Testövning 2.2
Skriv följande uttrck med högst ett rottecken:
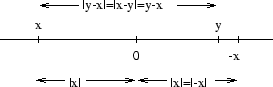
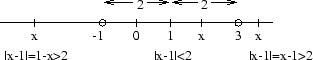
![]() Man söker de tal x sådana att avstånden till 1 och 3
samtidigt är mindre än eller lika med 5.
Man söker de tal x sådana att avstånden till 1 och 3
samtidigt är mindre än eller lika med 5. ![]() Man söker de tal x sådana att summan av avstånden
mellan x och 1 och x och 3 är mindre än eller lika med
5.
Man söker de tal x sådana att summan av avstånden
mellan x och 1 och x och 3 är mindre än eller lika med
5. ![]() Man söker de tal x sådana att summan av avstånden mellan
x och 1 och x och -3 är mindre än eller lika med
5.
Man söker de tal x sådana att summan av avstånden mellan
x och 1 och x och -3 är mindre än eller lika med
5.![]() .
.![]() Avståndet mellan x och 4 ska var lika med summan av 3 och avståndet
mellan x och 2.
Avståndet mellan x och 4 ska var lika med summan av 3 och avståndet
mellan x och 2. ![]() Förenklingen 3 + 2 = 5 ger att tolkningen blir: avståndet mellan
x och 4 ska vara lika med avståndet mellan x och - 5 .
Förenklingen 3 + 2 = 5 ger att tolkningen blir: avståndet mellan
x och 4 ska vara lika med avståndet mellan x och - 5 .![]() Avståndet mellan x och 4 ska vara lika med summan av 3 och avståndet
mellan x och - 2 .
Avståndet mellan x och 4 ska vara lika med summan av 3 och avståndet
mellan x och - 2 .