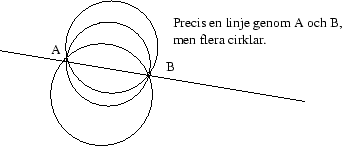
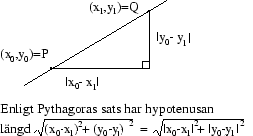En viktig princip för (räta) linjer är att en sådan bestäms av två av
dess punkter; genom två olika punkter går det precis en linjer.
Man kan kontrastera detta med cirklar; genom två givna punkter går det
oändligt många cirklar.
Om man har tre olika punkter A, B och C, hur ska man då kunna
avgöra om de ligger på en och samma linje?
Ett sätt är att resonera med hjälp area: Den trehörning (triangel) som
har A, B och C som hörn ska ha area noll.
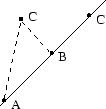
Ett annat sätt är att resonera med hjälp av avstånd: Det kortaste
avståndet mellan punkter är längs en linje. Om förhållandena är som i
figuren ovan betyder det att avståndet mellan C och A
ska vara summan av avstånden mellan C och B och B
och A, för att de tre punkterna ska ligga på samma linje.
Genom att införa ett koordinatsystem i planet, så att alla punkter får
koordinater, kan problemet lösas genom att man räknar med
hjälp av dessa koordinater.
Efter man infört ett koordinatsystem kan man tala om linjers
lutning eller riktningskoefficient. De linjer som saknar
riktningskoefficient är de som är parallella med y-axeln. För
övriga linjer definieras riktningskoefficienten som
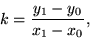
där ( x0 , y0 ) och
( x1 , y1 ) är punkter på linjen. Ett argument med
likformiga trianglar ger att detta är oberoende av vilka punkter
( x0 , y0 ) och
( x1 , y1 ) man väljer på linjen, och
att olika linjer genom punkten
( x0 , y0 ) har olika lutning.
För en tredje punkt ( x , y ) gäller att den ligger på
linjen genom ( x0 , y0 ) och
( x1 , y1 ) precis när denna linje har
samma lutning som linjen genom
( x0 , y0 ) och
( x , y ). Vi ska alltså ha
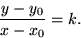
Efter multiplikation med x - x0 i båda led ger
detta
y = k( x - x0 ) + y0. Låter
vi nu m = -kx0 + y0, får vi att
( x , y ) ligger på linjen genom
( x0 , y0 ) och
( x1 , y1 ) precis när
y = kx + m
Man brukar säga att punkten ( x , y ) löser eller
satisfierar, ekvationen när detta inträffar. Vi kan sammanfatta detta
som
Linjen genom de två olika punkterna
( x0 , y0 ) och
( x1 , y1 ), där
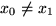 består precis av alla lösningar till ekvationen
y = kx + m, där k och m bestäms av
punkterna som ovan.
består precis av alla lösningar till ekvationen
y = kx + m, där k och m bestäms av
punkterna som ovan.
Villkoret
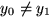 är med för om x0 = x1 så är linjen
genom punktena parallell med y-axeln och en sådan linje bestäms
av ekvationen x = m, där m = x0
(som inte är av formen y = kx + m ).
är med för om x0 = x1 så är linjen
genom punktena parallell med y-axeln och en sådan linje bestäms
av ekvationen x = m, där m = x0
(som inte är av formen y = kx + m ).
Man brukar därför tala om linjen y = kx + m
eller x = m, trots att det egentligen är fråga om
ekvationer. Observera att k anger linjens lutning och när
x = 0 ska y = m, så att linjen går genom
( 0 , m ). Talet m kan alltså avläsas som
y-koordinaten i skärningen mellan linjen och y-axeln.
Exempel 2.7
Bestäm (ekvationen för) linjen som går genom punkterna med
koordinater ( 1 , 2 ) respektive ( -3 ,4 ) . Vi vet att linjen är av
formen y = kx + m och inte av formen
x = m eftersomm de båda punkterna har olika
x -koordinater. Uppgiften är att bestämma k och m
Det finns nu två lite olika sätt att lösa problemet på. Välj
alternativ!
 Med hjälp av formlerna för k och m ovan
Med hjälp av formlerna för k och m ovan
 Utan formler
Utan formler
Vi har, om vi sätter
( x0 , y0 ) = ( 1 , 2 ) och
( x1 , y1 ) = ( -3 , 4 ) att
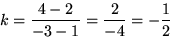
och
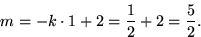
Linjens ekvation är alltså y = -x/2 + 5/2. Kontrollera detta
genom att se att punkterna ( 1 , 2 ) och ( -3 , 4 ) satisfierar ekvationen!
Vi vet att ( 1 , 2 ) och ( -3 , 4 ) ligger på linjen y = kx + m, så
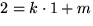 och 4 = k(-3) + m. Vi ska bestämma
k och m så att dessa båda likheter gäller samtidigt,
d.v.s vi ska lösa ekvationssystemet
och 4 = k(-3) + m. Vi ska bestämma
k och m så att dessa båda likheter gäller samtidigt,
d.v.s vi ska lösa ekvationssystemet

Om vi subtraherar den undre ekvationen från den övre får vi 4k=-2,
eller k=-1/2. Om vi multiplicerar den övre ekvationen med 3 så
att den blir 3k+3m=6 och adderar den undre får vi
4m=10 , eller m=5/2.
Linjens ekvation är alltså
y = -x/2 + 5/2. Kontrollera att punkterna ( 1 , 2 ) och ( -3 , 4 )
löser denna ekvation!
Exempel 2.8 Avgör om punkerna
( -1 , 2 ) , ( 1 , 3 ) och ( 13 , 17 / 2 ) ligger på en linje.
Eftersom
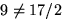 ligger punkten ( 13 , 17 / 2 ) inte på linjen genom ( -1 , 2 ) och
( 1 , 3 ).
ligger punkten ( 13 , 17 / 2 ) inte på linjen genom ( -1 , 2 ) och
( 1 , 3 ).
Testövning 2.3Bestäm ekvationen på formen
y = kx + m, eller x = m, för linjen genom
de två första av följande punkter. Avgör också om punkterna ligger på
en linje.
Ofta är det bekvämt att skriva linjens ekvation på en lite annorlunda
form. Om ekvationen y = kx + m multipliceras med en
konstant
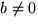 får man en ekvation, by = bkx + bm, med precis samma
lösningar som den ursprungliga. Sätter vi nu a = -bk och
c = bm får vi
får man en ekvation, by = bkx + bm, med precis samma
lösningar som den ursprungliga. Sätter vi nu a = -bk och
c = bm får vi
ax + by = c,
som alltså
också är en ekvation för den ursprungliga linjen. Fördelen med detta
skrivsätt är dels att variablerna ( x och y ) står på
samma sida, dels att om vi väljer b = 0 och
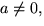 så får vi linjen x = c / a. Varje linje har
alltså en ekvation av formen ax + by = c, där
a, b och c är konstanter. Nackdelen är att en och
samma linje nu kan beskrivas av olika ekvationer (även om
dessa förstås har samma lösningar). T.ex. beskriver ekvaitonerna
x-2y=3, -2x+4y=-6 och
2x-4y=6 alla linjen y = x/2-3/2 genom
(0 ,-3/2) med riktningskoefficient 1/2.
så får vi linjen x = c / a. Varje linje har
alltså en ekvation av formen ax + by = c, där
a, b och c är konstanter. Nackdelen är att en och
samma linje nu kan beskrivas av olika ekvationer (även om
dessa förstås har samma lösningar). T.ex. beskriver ekvaitonerna
x-2y=3, -2x+4y=-6 och
2x-4y=6 alla linjen y = x/2-3/2 genom
(0 ,-3/2) med riktningskoefficient 1/2.
Exempel 2.9 Vilken riktningskoefficient har linjen
2
x - 5
y = -2 och i vilken punkt skär linjen
y -axeln?
Om vi skriver linjen på formen y = kx +
m , så är
riktningskoefficienten k och skärningspunkten med
y -axeln ( 0 , m ).
Vi subtraherar 2x i
ekvationens båda led och får -5y = -2x - 2 . Division med -5
ger en ekvation med samma lösningar som den ursprungliga ekvationen:
y = 2x / 5 + 2 / 5 .
Linjens riktningskoefficient är alltså 2/5 och skärningspunkten med
y -axeln är ( 0 , 2 / 5 ).
Testövning 2.4 Bestäm
riktningskoefficienten för följande linjer
och avgör om det finns en punkt med y -koordinat 1 på dem. Ange den
i så fall.
En fundamental egenskap för två linjer i planet är att precis ett av
följande fall inträffar:
- 1.
- de skär varandra inte (d.v.s de är parallella men
ej sammanfallande),
- 2.
- de skär varandra i precis en punkt (den så kallade
skärningspunkten),
- 3.
- de sammanfaller (d.v.s de är en och samma linje)
Exempel 2.10
Vilket av fallen inträffar för de två linjerna
2
x + 3
y = -5 och 4
x + 6
y = 7 ?
Det finns (åtminstonde) två möjliga strategier för att avgöra detta. Välj en!
 Med hjälp av riktningskoefficienter.
Med hjälp av riktningskoefficienter.
 Med hjälp av ekvationerna direkt.
Med hjälp av ekvationerna direkt.
Linjen 2x + 3y = -5 bestäms också av ekvationen
y = -2x/3 - 5 / 3 . Linjen 4x + 6y = 7 bestäms också
av linjen y = -4x / 6 + 7 / 6 = -2x / 3 + 7 / 6
. Vi ser att båda
linjerna har lutningen -2 / 3 (riktningskoefficient). Den första går
genom punkten ( 0 , -5 / 3 ), medan den andra skär y -axeln i punkten
( 0 , 7 / 6 ). Eftersom
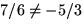 skär linjerna inte varandra.
Vi undersöker om det finns någon punkt ( x , y ) som löser
båda ekvationerna. Vi ska alltså lösa ekvationssystemet
skär linjerna inte varandra.
Vi undersöker om det finns någon punkt ( x , y ) som löser
båda ekvationerna. Vi ska alltså lösa ekvationssystemet
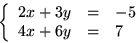
Om vi multiplicerar den översta ekvationen med 2 och subtraherar den
från den nedersta (så att x försvinner) får vi ekvationen
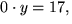 som ju saknar lösning. Det finns alltså ingen punkt som ligger på båda
linjerna.
som ju saknar lösning. Det finns alltså ingen punkt som ligger på båda
linjerna.
Den andra av dessa båda metoder är att föredra om man inte bara vill
svara på frågan om vilket av de tre fallen som inträffar, utan också
är intresserad av att bestämma skärningspunkten om det är fall 2 som
gäller.
Exempel 2.11 Undersök vilket av de
tre fallen som gäller för linjerna 2
x - 4
y = 5 och
3
x + 6
y + 1 = 0 . Bestäm skärningspunkten om det är fall 2 som
gäller.
Observera att den andra linjens ekvation skrivits så att
man har noll i ena ledet. Linjen är den samma som den som bestäms av
3x + 6y = -1 (subtrahera 1 i båda leden).
Även om det inte är nödvändigt, kan vi genast inse att att linjerna
har de olika riktningskoefficienter 2 respektive -2 och att de därför
kommer att skära varandra i precis en punkt.
Vi söker gemensamma lösningar ( x , y ) till de båda
ekvationerna och ska därför lösa ekvationssystemet
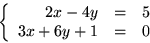
Om vi multiplicerar den övre ekvationen med 3 och den nedre med -2 och
adderar resultaten kommer vi att få en ekvation som inte innehåller
x:
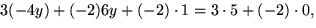
som vi kan hyfsa till -24
y = 17, d.v.s
y = -17 / 24. För att
bestämma
x kan vi nu t.ex. sätta in
y = -17 / 24 i de båda
ekvationerna och se att de då har en gemensam lösning
x.
Vi kan också använda samma metod som vi använde för att bestämma
y: multiplicerar vi den översta ekvationen med 3 och den undre
med 2 får vi en ekvation utan y:
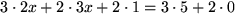 .
Omskrivning ger nu 12x = 13, så att x = 13 / 12 .
.
Omskrivning ger nu 12x = 13, så att x = 13 / 12 .
Kontroll visar att punkten (13 / 12,-17 / 24) verkligen löser
ekvationssystemet. Vi har alltså insett att de båda linjerna skär
varandra i precis en punkt, nämligen (13 / 12,-17 / 24).
Exempel 2.12 Avgör hur linjerna
2x - 3y = 5 och 4x - 3y = 7 skär varandra. Om de
skär varandra i precis en punkt, bestäm denna.
Hur vill du börja?
 Först avgöra vilket av fallen 1-3 som inträffar
Först avgöra vilket av fallen 1-3 som inträffar
 Direkt försöka bestämma skärningen mellan linjerna
Direkt försöka bestämma skärningen mellan linjerna
Linjerna skär alltså varandra i precis en punkt. Det gäller nu att
bestämma denna. Detta kan göras med hjälp av ekvationssystemet
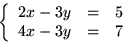
Kontrollera nu att den punkt du fått ligger på de båda linjerna!
Det gäller att undersöka hur många gemensamma punkter linjerna
har. Detta antal kan vara ingen, precis en, eller oändligt många.
De gemensamma punkterna satisfierar ekvationssystemet
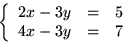
och det gäller att lösa detta.
Testövning 2.5
Avgör hur följande par av linjer skär varandra och bestäm
skärningspunkten i förekommande fall.
a) 7x - 3y = -2 och 3x - 2y = 2.
 De skär varandra i en punkt.
De skär varandra i en punkt.
 De sammanfaller.
De sammanfaller.
 De är parallella men inte sammanfallande.
De är parallella men inte sammanfallande.
b) 91x - 77y = 2 och 13x + 3 = 11y.
 De skär varandra i en punkt.
De skär varandra i en punkt.
 De sammanfaller.
De sammanfaller.
 De är parallella men inte sammanfallande.
De är parallella men inte sammanfallande.
c) 15x - 3y = 3 och 12x + 7y = 40.
 De skär varandra i en punkt.
De skär varandra i en punkt.
 De sammanfaller.
De sammanfaller.
 De är parallella men inte sammanfallande.
De är parallella men inte sammanfallande.
Om en linje ges av ekvationen ax + by = c, hur ser då
ekvationen ut för en linje som är vinkelrät mot denna?
Frågan är lätt att besvara för
linjerna x = c och y = c, d.v.s för linjer
parallella med y - axeln respektive x - axeln. En linje
vikelrät mot x = c måste vara parallell med x - axeln
och har därför en ekvation av formen y = d, där d
är någon konstant. En linje vinkelrät mot y = c måste, på
samma vis, ha en ekvation av formen x = d, där d är
en konstant.
Vi börjar med att fundera på vilken riktningskoefficient en sådan
linje måste ha. Vi skriver först den ursprungliga linjens ekvation på
formen y = kx + m, genom att dividera ekvationen
ax + by = m med b och döpa om
konstanterna. (Detta är bara möjligt om
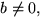 men om b = 0 , så är linjen parallel med y - axeln och vi har
redan förstått hur ekvationen för en linje som är vinkelräta mot en
sådan ser ut.)
men om b = 0 , så är linjen parallel med y - axeln och vi har
redan förstått hur ekvationen för en linje som är vinkelräta mot en
sådan ser ut.)
 Fortsätt!
Fortsätt!
Vi ritar en figur där
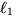 är linjen med ekvation y = kx + m och
är linjen med ekvation y = kx + m och
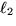 är en linje vinkelrät mot denna.
Låt P vara linjernas skärningspunkt. Drag en linje parallell
med x - axeln genom P och en linje parallell med
y - axlen till höger om punkten.
I figuren har det nu uppstått en större rätvinklig triangel och två
mindre.
är en linje vinkelrät mot denna.
Låt P vara linjernas skärningspunkt. Drag en linje parallell
med x - axeln genom P och en linje parallell med
y - axlen till höger om punkten.
I figuren har det nu uppstått en större rätvinklig triangel och två
mindre.
Eftersom vinkelsumman i en triangel är 180 grader är
 lika med 90 grader liksom
lika med 90 grader liksom
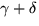 .
Men också
.
Men också
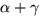 är 90 grader eftersom linjerna skär varandra vinkelrätt.
är 90 grader eftersom linjerna skär varandra vinkelrätt.
Vi ser alltså att
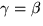 och
och
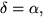 så att de tre trianglarna i figuren är likformiga och rätvinkliga.
så att de tre trianglarna i figuren är likformiga och rätvinkliga.
Inför nu längderna r, p och q som i figuren. Så
som figuren är ritad har
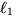 riktningskoefficienten k = p / r. (Om vi ritat den
med negativ lutning, skulle den varit k = -p / r.)
riktningskoefficienten k = p / r. (Om vi ritat den
med negativ lutning, skulle den varit k = -p / r.)
Linjen
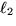 har riktningskoefficient -q / r. Men eftersom de små
trianglarna är likformiga har vi att
q /r = r / p = 1 / k
har riktningskoefficient -q / r. Men eftersom de små
trianglarna är likformiga har vi att
q /r = r / p = 1 / k
Vi har kommit fram till:
En linje vinkelrät mot y = kx + m har en
ekvation av formen y = -x / k + n, där
n är en konstant.
Om vi nu går tillbaka till ekvationen av formen
ax + by = c så har linjen riktningskoefficient
-a / b (Vi förutssätter att
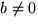 )
)
En linje vinkelrät mot denna har därför en ekvation av formen
y = bx / a + n. Multiplicerar vi nu med a
och sätter na = d får vi
-bx + ay = d. Detta gäller även om b = 0 !
En linje vinkelrät mot ax + by = c har
en ekvation av formen -bx + ay = d där d är
en konstant.
Exempel 2.13
Antag att P = ( -1 , 2 ) och Q = ( 2 , -16 ) och
R = ( 1 , 1 ). Bestäm en ekvation för linjen genom R som är vinkelrät
mot linjen genom Q och R
Hur tycker du man ska börja?
 Bestäm först linjen genom P och R
Bestäm först linjen genom P och R
 Bestäm först mittpunkten mellan P och Q
Bestäm först mittpunkten mellan P och Q
 Bestäm först linjen genom P och Q
Bestäm först linjen genom P och Q
Vi bestämmer först en ekvation y = kx + m för linjen
genom P och Q, som vi direkt av deras
x - koordinater inser inte är parallell med y - axeln. På så
vis får vi reda på att den sökta linjen genom R har en ekvation
av formen y = -x / k + n. Har vi väl bestämt
k så kan vi utnyttja att denna linje går genom (1,1) för att
bestämma n. Men först alltså linjen genom P och
Q. Eftersom y = kx + m ska ha lösningarna
P = ( -1 , 2 ) och Q = ( 2 , -16 ) får vi ekvationssystemet

För att bestämma talet n ska vi utnyttja att
 linjen vi söker är vinkelrät
mot linjen y = -6x - 4
linjen vi söker är vinkelrät
mot linjen y = -6x - 4
 linjen vi söker går genom ( 1 , 1 )
linjen vi söker går genom ( 1 , 1 )
Testövning 2.6
Avgör om följande par av linjer är vinkelräta mot varandra:
a) Linjerna 2x + 3y = 5 och 6x - 4y = 2.
 Ja
Ja
 Nej
Nej
b) Linjerna geonom ( 1 , 1 ) och ( 2 , 3 ) respektive ( -1 , 1 ) och
( 0 , -1/2 ) .
 Ja
Ja
 Nej
Nej
c) Linjen 2x - 3y = 1 och linjen genom ( -1 , 1 ) och
( 2 , 1 / 3 ) .
 Ja
Ja
 Nej
Nej
Testövning 2.7
Bestäm ekvationen för linjen som går genom punkten
(Det kortaste) avståndet mellan två punkter
P0 = ( x0 , y0 ) och
P1 = ( x1 , y1 ) i
planet definieras som
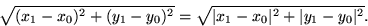
Motiveringen till denna definition ges av Pythagoras sats:
Testövning 2.8
Bestäm avståndet mellan punkterna (förenkla om möjligt!)
För att beräkna (det kortaste) avståndet mellan en punkt
P = ( x0 , y0 ) och en linje
ax + by = c kan man igen utnyttja Pythaggoras
sats:
Vi ser att vi ska bestämma skärningspunkten
Q = ( x1 , y1 ) mellan linjen
ax + by = c och linjen vinkelrät mot denna genom
P. Avståndet är sedan avståndet mellan punkterna P och
Q. En annan punkt R på linjen har ett större avstånd
till P, enligt Pythagoras sats.
Exempel 2.14
Bestäm avståndet mellan punkten ( 5 , -4 ) och linjen
3x - 2y = 10.
En linje vinkelrät mot
3x - 2y = 10 har en ekvation av formen
2x + 3y = n. Av dessa linjer går den som har
-2=n genom P = ( 5 , -4 ) och den har alltså ekvationen
3x + 2y = -2 .
För att bestämma skärningspunkten Q
mellan de två linjerna ska vi lösa ekvationssystemet
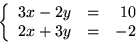
Testövning 2.9
Bestäm avståndet mellan

![]()
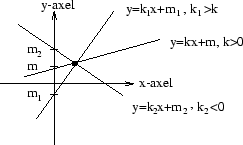
![]()
består precis av alla lösningar till ekvationen y = kx + m, där k och m bestäms av punkterna som ovan.
![]() är med för om x0 = x1 så är linjen
genom punktena parallell med y-axeln och en sådan linje bestäms
av ekvationen x = m, där m = x0
(som inte är av formen y = kx + m ).
är med för om x0 = x1 så är linjen
genom punktena parallell med y-axeln och en sådan linje bestäms
av ekvationen x = m, där m = x0
(som inte är av formen y = kx + m ).![]() Med hjälp av formlerna för k och m ovan
Med hjälp av formlerna för k och m ovan ![]() Utan formler
Utan formler ![]()
![]()
![]() och 4 = k(-3) + m. Vi ska bestämma
k och m så att dessa båda likheter gäller samtidigt,
d.v.s vi ska lösa ekvationssystemet
och 4 = k(-3) + m. Vi ska bestämma
k och m så att dessa båda likheter gäller samtidigt,
d.v.s vi ska lösa ekvationssystemet
![]()
![]() ligger punkten ( 13 , 17 / 2 ) inte på linjen genom ( -1 , 2 ) och
( 1 , 3 ).
ligger punkten ( 13 , 17 / 2 ) inte på linjen genom ( -1 , 2 ) och
( 1 , 3 ).
![]() får man en ekvation, by = bkx + bm, med precis samma
lösningar som den ursprungliga. Sätter vi nu a = -bk och
c = bm får vi
får man en ekvation, by = bkx + bm, med precis samma
lösningar som den ursprungliga. Sätter vi nu a = -bk och
c = bm får vi
![]() så får vi linjen x = c / a. Varje linje har
alltså en ekvation av formen ax + by = c, där
a, b och c är konstanter. Nackdelen är att en och
samma linje nu kan beskrivas av olika ekvationer (även om
dessa förstås har samma lösningar). T.ex. beskriver ekvaitonerna
x-2y=3, -2x+4y=-6 och
2x-4y=6 alla linjen y = x/2-3/2 genom
(0 ,-3/2) med riktningskoefficient 1/2.
så får vi linjen x = c / a. Varje linje har
alltså en ekvation av formen ax + by = c, där
a, b och c är konstanter. Nackdelen är att en och
samma linje nu kan beskrivas av olika ekvationer (även om
dessa förstås har samma lösningar). T.ex. beskriver ekvaitonerna
x-2y=3, -2x+4y=-6 och
2x-4y=6 alla linjen y = x/2-3/2 genom
(0 ,-3/2) med riktningskoefficient 1/2.