Antag att vi har två vektorer u och v, så att
(åtminstone) u 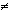 0.
0.
Det finns då precis en vektor p som uppfyller följande två villkor
1) p är parallell med u
2) v - p är orotogonal mot u
Om p uppfyller villkoren gäller enligt 1) att
p = tu, för något reellt tal
t.
 Tar vi skalärprodukt med u får vi
Tar vi skalärprodukt med u får vi
p·u = t|u|2
Å andra sidan ger 2) att
(v - p)·u = 0
så
p·u = v·u.
Tillsammans ger detta att
Det betyder att
så vi ser att det bara kan finnas en vektor p som uppfyller
villkoren 1) och 2). Å andra sidan kontrollerar man lätt att denna
vektor p verkligen satisfierar 1) och 2). (Gör det!)
Vektorn
kallas den vinkelräta projektionen av vektorn
v längs
u.
Exempel 3.1.1
Bestäm den orotgonala projektionen av vektorn
( -1, 2, 2) längs vektorn ( 1, -2, 2).
Vi sätter v = ( -1, 2, 2) och
u = ( 1, -2, 2) och ska beräkna
p = (v·u / |u|2)u
Vi har
Det betyder att
Exempel 3.1.2
Man vet att vektorn v har den vinkelräta projektionen
p = ( 1/3, -4/3, 2/3) längs vektorn
u = ( -1, 4, -2).
Bestäm alla möjliga värden på v.
Vi observerar först att p = (-1/3)u, så att
uppgiften är meningsfull. (Den vinkelräta projektionen av v
längs u ska ju vara parallell med u.)
Vi ska alltså bestämma alla vektorer v, så att
Utnyttjar vi nu att vi känner u och p och tar
skalärprodukt med u får vi (och detta är enda villkoret på v)
Detta ger att de vektorer
v = ( x, y, z)
som vi söker är de vars koordinater löser ekvationen
-x + 4y - 2z = -7
Vi har tidigare sett att lösningarna till en sådan ekvation ges av
ett plan i rummet. Den geometriska tolkningen av detta är att
mängden av de punkter
P = ( x, y, z),
sådana att vektorn v = OP uppfyller villkoret i uppgiften bildar ett
plan i rummet. Geometrisk sett är detta uppenbart.
uppfyller villkoret i uppgiften bildar ett
plan i rummet. Geometrisk sett är detta uppenbart.
Bestäm en parameter framställning till detta plan
genom att sätt x = t och
y = s;
Testövning 3.1.1
a) Bestäm den ortogonala projektionen p av vektorn
v = ( -2, 2, 3) längs vektorn
u = ( 1, 2, 3)
b) Om vektorn w = ( x, y)
vet man att den ortogonala projektionen längs
u = ( 1, 2) och
v = ( -3,-2) är ( 1/2, 1) respektive
( 3, 2). Bestäm vektorn w.
Svar:
c) Antag att de tre vektorerna u, v och w
uppfyller följande villkor:
1) w och u har samma ortogonala projektion längs v
2) w och v har samma ortogonala projektion längs u
Visa att w är vinkelrät mot u - v.
 Hjälp
Hjälp
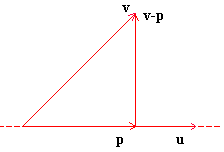
Antag att L är en linje och Q är en punkt vilken som
helst.
Då finns det precis en punkt F så att följande gäller:
1)
F ligger på
L
2) vektorn
FQ
är orotgonal mot
L
Att en vektor u är ortogonal mot en linje betyder att den är
ortogonal mot en riktningsvektor för linjen. (Den är då också
ortogonal mot varje riktningsvektor för linjen efter som alla
sådana är parallella.)
Välj nämligen en punkt P0 på linjen och en riktiningsvektor
v för den. Enligt 1) ska vi, för att bestämma F, söka
t så att
OF
=
OP0
+
tv
Vi har då, enligt 2, att
ska vara ortogonal mot v. Skalärprodukt med v ger alltså
0 =
P0Q
·
v -
t|
v|
2
så att t = (P0Q ·v) / |v|2.
Därmed har vi (entydigt) bestämt t, och därmed F, så att
1) och 2) gäller.
·v) / |v|2.
Därmed har vi (entydigt) bestämt t, och därmed F, så att
1) och 2) gäller.
Exempel 3.1.3
Låt L vara linjen med parameterframställningen
( x, y, z) = ( -3, -3, 8) + t( 2, 2, -4).
Bestäm den ortogonala projektionen av punkten
Q = ( 2, 2, 1) på linjen L.
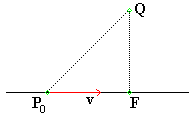
Vi börjar med att välja en punkt P0 på linjen. Vi
väljer den (t.ex.) genom att sätta t = 0 i
parameterframställningen:
P0 = ( -3, -3, 8). Vi
väljer sedan en riktningsvektor v för linje till (t.ex)
v = ( 1, 1, -2)
Låt
Pt = ( -3 + 2t, -3 + 2t, 8 - 4t)
vara en godtycklig punkt på linjen. Vår uppgift är att bestämma
t (och därmed den ortogonala projektionen F = Pt av
Q), så att vektorerna v och PtQ = ( 5 - 2t, 5 - 2t, -7 + 4t)
är ortogonala.
= ( 5 - 2t, 5 - 2t, -7 + 4t)
är ortogonala.
Vi får
Den sökta punkten F är nu punkten Pt, där
vi väljer t = 2, som ju är lösningen till
ekvationen ovan. Svaret blir allstå punkten ( 1, 1, 0).
Exempel 3.1.4
Vísa analytiskt att mängden av de punkter Q i rummet som har
den ortogonala projektion ( 5, 1, 10) på linjen
( 1 - 2t, 3 + t, 2 - 4t),
utgör ett plan i rummet.
Geometriskt är det uppenbart att detta stämmer! Låt oss se om vi kan
inse detta analytiskt också. Ett sätt att visa påståendet i exemplet
är att skriva upp en parameterframställning av ett plan vars punkter
består precis av de Q som uppfyller förutsättningen i exemplet.
För att åstadkomma detta låter vi först
Q = ( x, y, z),
vara en punkt vilken som helst i rummet. Vi är intresserade av att
finna villkor på koordinaterna så att denna punkt har den ortogonala
projektionen F = ( 5, 1, 10) på linjen i exemplet.
Det betyder att vi ska bestämma x, y och z så
att vektorerna
FQ
= (
x - 5,
y - 1,
z - 10)
och
v ( -2, 1, -4) (riktningsvektor för linjen)
är ortogonala. Detta ger ekvationen
Sätter vi nu (t.ex) x = t och
z = s ser vi att de punkter som söks i
exemplet är de
Q = ( x, y, z)som
är av formen
x = t
y = 2t + 4s - 49
z = s
Vi har de två riktningsvektorerna ( 1, 2, 0) (som hör
till t) respektive
( 0, 4, 1) (som hör till s), som inte är
parallella. Det betyder att detta är en parameterframställning för ett
plan i rummet.
Testövning 3.1.2
a) Bestäm den ortogonala projektionen av punkten
Q = (1, -2, 5) på linjen
( 4 + 2t, 5 + t, 4 + t).
b) Om punkten Q vet man att dess ortogonala projektion på
linjen
( -2 + 2t, 2t, -2 + t)
är ( 0, 2, -1) medan dess ortogonala projektion på
linjen
( -1 + 2t, -3 + t, -1 + t)
är ( 3, -1, 1). Hur många lösningar har problemet?
 Oänligt många
Oänligt många
 Ändligt många
Ändligt många
 Inga
Inga
Vilket är det minsta antal parametrar som krävs för att beskriva
samtliga lösningar Q?
 En
En
 Två
Två
Bestäm Q (använd parametrern s).
c) Finns det någon linje i rummet så att de tre punkterna
( 1, 2, 3), ( 2, 4, 5) och
( 1, 4, 3) har samma ortogonala projektion på denna
linje?
 Ja, oändligt många
Ja, oändligt många
 Ja, precis en
Ja, precis en
 Nej, ingen
Nej, ingen
Vad blir den (gemensamma) ortogonala projektionen om man bland dessa
linje väljer den (enda) som går genom origo?
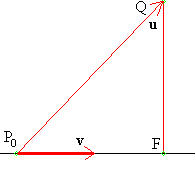 Vi vill bestämma (det minsta) avståndet mellan en punkt
Q = ( x, y, z)
och en punkt på linjen linjen med parameterframställning
P0 + tv. Vi antar att
P0 = ( x0, y0, z0).
Vi låter P0Q
Vi vill bestämma (det minsta) avståndet mellan en punkt
Q = ( x, y, z)
och en punkt på linjen linjen med parameterframställning
P0 + tv. Vi antar att
P0 = ( x0, y0, z0).
Vi låter P0Q = u. Avståndet i kvadrat mellan punkten
P0 + tv på linjen och
punkten Q är då
= u. Avståndet i kvadrat mellan punkten
P0 + tv på linjen och
punkten Q är då
| tv - u |2 = ( tv - u)·( tv - u) =
= t2| v |2 - 2tv·u + | u |2.
För att inse vad det minsta värdet som detta uttryck antar (när
t varierar) gör vi en kvadratkomplettering och får
(| v |t - v·u / | v |)2 - (v·u / | v |)2 + | u |2.
Enligt Cauchy-Schwartz olikhet är
-(v·u / | v |)2 + | u |2 > 0.
Det betyder att det förra uttrycket antar sitt minsta värde när vi väljer
t = u·v / | v |2.
Den punkt på linjen som ligger närmast punkten Q är alltså
P0 + (u·v / | v |2) v,
dvs den ortogonala projektionen av Q på linje. Avståndet i
kvadrat mellan denna punkt och Q är
| u |2 - (v·u / | v |)2
Detta avstånd kallas (det minsta) avståndet mellan punkten Q
och linjen P0 + tv.
Exempel 3.1.5
Bestäm avståndet mellan punkten ( 4, 1, -3) och linjen
som går genom de två punkterna ( 5, 4, 2) och
( 8, 5, 3).
Även om vi skulle kunna använda formeln ovan direkt gör vi i stället
så att vi först bestämmer den orogonala projektionen
F av
punkten
Q = ( 4, 1, -3) på
linjen. Sedan ges avståndet mellan punkten
Q och linjen av
avståndet mellan punkterna
Q och
F.
En riktningsvektor för linjen ges av
v = ( 8 - 5, 5 - 4, 3 - 2) = ( 3, 1, 1).
En godtycklig punkt på linjen kan alltså skrivas
( 5, 4, 2) + t( 3, 1, 1).
För att detta ska vara F ska vi bestämma t, så att
vektorn
( 4 - 5, 1 - 4, -3 - 2)- t( 3, 1, 1)
är orotgonal mot vektorn ( 3, 1, 1). Detta ger oss ekvationen
0 = ( -1 -3t)·3 + ( -3 - t)·1 + ( -5 - t)·1 =
som föreklas till 0 = -11t - 11, eller
t = -1. Detta ger oss
F = ( 5 - 3, 4 - 1, 2 - 1) = ( 2, 3, 1).
Avståndet mellan Q = ( 4, 1, -3) och
F (och därmed mellan Q och linjen) är alltså
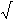
(( 4 - 2)
2 + ( 1 - 3)
2 + ( -3 - 1)
2) = 2
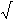
6.
Om vi i exemplet i stället använder oss av formeln vi kom fram till
ovan, har vi v = ( 3, 1, 1) och
u = ( 4 - 5, 1 - 4, -3 - 2) = ( -1, -3, -5)
och vi får att avståndet är
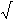
( 1 + 9 + 25 - ( -11)
2 / ( 11)) =
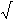
24 = 2
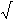
6.
Formler är användbara i teoretiska sammanhang men också i
praktiken. Nackdelen med formler är att de är svåra att komma
ihåg. Det är lättare att komma ihåg en ide´. I vårat fall är det
lättare att komma ihåg att avståndet mellan en linje och en punkt är
avståndet mellan punkten och dess ortogonala projektion på linjen, än
att komma ihåg formeln för hur detta avstånd kan beräknas!
Testövning 3.1.3
a) Bestäm avståndet mellan punkten ( 1, 2, 3) och
linjen med parameterframställningen ( 0, -5, 1) + t( 1, 1, 2)
Svar:
b) Finns det någon linje, som går genom origo, sådan att avståndet
till punkten ( 1, 2, 3) är samma som avståndet till ( 3, 2, 1)?
 Ja, oändligt många
Ja, oändligt många
 Ja, precis en
Ja, precis en
 Nej, ingen
Nej, ingen
c) Finns det någon linje i rummet så att avståndet till punkten
( -2, 0, 3) är 5 medan avståndet till
( 1, 1, 2) är 15?
 Ja, oändligt många
Ja, oändligt många
 Ja, precis en
Ja, precis en
 Nej, ingen
Nej, ingen
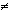 0.
0. Tar vi skalärprodukt med u får vi
Tar vi skalärprodukt med u får vi![]() uppfyller villkoret i uppgiften bildar ett
plan i rummet. Geometrisk sett är detta uppenbart.
uppfyller villkoret i uppgiften bildar ett
plan i rummet. Geometrisk sett är detta uppenbart.
 Vi vill bestämma (det minsta) avståndet mellan en punkt
Q = ( x, y, z)
och en punkt på linjen linjen med parameterframställning
P0 + tv. Vi antar att
P0 = ( x0, y0, z0).
Vi låter P0Q
Vi vill bestämma (det minsta) avståndet mellan en punkt
Q = ( x, y, z)
och en punkt på linjen linjen med parameterframställning
P0 + tv. Vi antar att
P0 = ( x0, y0, z0).
Vi låter P0Q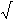 (( 4 - 2)2 + ( 1 - 3)2 + ( -3 - 1)2) = 2
(( 4 - 2)2 + ( 1 - 3)2 + ( -3 - 1)2) = 2