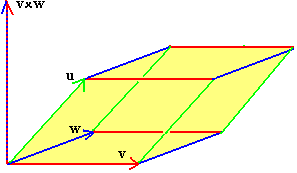
Tre vektorer i rummet som inte ligger i ett och samma plan spänner tillsammans vad som kallas en parallellepiped. Om dessa vektorer kallas  u, v  respektive  w  kan volymen  V  av parallellepipeden beräknas med formeln
V = | u · ( vw) |    Detaljer

 
Exempel 4.3.1
 
Beräkna volymen av den parallellepiped som spänns av vektorerna  u = ( 1, 2, 3) ,  v = ( 1, 2, 4)  och  w = ( 2, 1, 3).
 
Formeln ger oss att volymen blir absolutbeloppet av

1 ·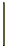 2   4
1   3 		- 2 1   4
2   3 		+ 3 1   2
2   3

Efter förenkling blir volymen alltså

     

 
Den geometriska tolkningen av absolutbeloppet av uttrycket  u · ( vw)  kan vara användbart för att visa påståenden om kryss- och skalärprodukter.
 
Exempel 4.3.2
 
Låt  u ,  v  och  w  vara tre vektorer i rummet. Visa att

 u · ( vw) = (uv) · w

Absolutbeloppet av de båda talen är lika eftersom detta ger två olika sätt att beräkna volymen av den parallellepiped som spänns av vektorerna. Det gäller alltså bara att inse att de två talen har samma tecken.
Vänstra ledet är positivt precis när vektorerna  v, w  och  u  (i denna ordning!) bildar ett högersystem.
Högra ledet är positivt precis när vektorerna  u, v  och  w  (i denna ordning!) bildar ett högersystem.
Med hjälp av höger hands tumme, pekfinge och långfinger ser vi att  v, w  och  u  är ett högersystem precis när  u, v  och  w  också är det.
Alltså är de två båda talen positiva när ett av dem är det (och därmed negativa när ett av dem är det). De två talen måste med andra ord ha samma tecken.


 
Testövning 4.3.1
 
a) Beräkna volymen av en parallellepiped som spänns av vektorerna  ( 1, 1, 0) ,  ( 2, -1, 1)  och  ( 2, 0, 1) .
 
Svar:   
b) Låt  u ,  v  och  w  vara tre vektorer i rummet. Visa att

u( vw ) = ( u · w )v - ( u · v ) w

genom att t.ex. använda resultatet i exemplet ovan.
 
Hjälp En "tre gånger tre" -matris ( 33 -matris) är ett kvadratiskt schema av tal av formen

a1   b1   c1
a2   b2   c2
a3   b3   c3

Med determinanten till en sådan 33 -matris menas talet
        a1   b1   c1
a2   b2   c2
a3   b3   c3
 = a1  b2   c2
 b3   c3
 - a2  b1   c1
 b3   c3
 + a3  b1   c1
 b2   c2
Determinantens absolutbelopp är med andra ord volymen av den parallellepiped som spänns av vekotererna med koordinater  ( a1, a2, a3) ,  ( b1, b2, b3)  och ( c1, c2, c3) .
 
Man skriver ibland (när  u,  v och  w är vektorer i rummet)
       det( u, v, w) 
för den determinant vars tre rader är koordinaterna för de tre vektorerna (i tur och ordnng). Vi har då att  det( u, v, w) = u · ( vw) .
 

Exempel 4.3.3
 
Beräkna determinanten
        2   -1    3
3     2    1
4   -2   -2

Enligt definitionen är detta alltså
2   2    1
-2   -2 		- 3 -1    3
-2   -2 		+ 4 -1   3
  2   1
som blir  2(-2) - 3·8 + 4(-7) = -56.

 
Determinanter av typ  33  kan också beräknas med vad som brukar kallas Sarrus regel. Det går till på det viset att man skriver upp de två första kolonnerna en gång till och sedan multiplicerar ihop talen längs de diagonaler som bildas. För diagonaler med "negativ" lutning använder man ett plustecken, för de med "positiv" använder man ett nimustecken. Sedan summeras allt:
Längs de röda diagonalerna får vi produkterna

a1b2c3, b1c2a3  respektive  c1a2b3 

Längs de gröna diagonalerna får vi produkterna

- a3b2c1, - b3c2a1  respektive  - c3a2b1, 

Summan av dessa ger determinantens värde:
  a1   b1   c1
a2   b2   c2
a3   b3   c3
 = a1b2c3 + b1c2a3 + c1a2b3 - a3b2c1 - b3c2a1 - c3a2b1.
Att detta stämmer kontrollerar man genom att skriva ut vad definitionen ger och se att det är precis vad som stör i högra ledet i likheten ovan.
 

Exempel 4.3.4
 
Beräkna determinanten
        2     1    2
2     3    0
1   -4   -1
Sarrus regel ger att determinatens värde är

2·3·(-1) + 1·0·1 + 2·2·(-4) - 1·3·2 - (-4)·0·2 - (-1)·2·1 =
 = -6 + 0 - 16 - 6 + 0 + 2 = -26.


 
För  33 -matirser gäller liknande räkneregler som för  22 -matirser.
 
  1. Determinanten är additiv i raderna. Se vad detta betyder!
  2. Om en rad multipliceras med ett tal t och addras till en annan rad ändras inte determinantens värde. Se detta med symboler!
  3. Om två rader byter plats byter determinanten tecken. Se detta med symboler!
  4. Om en rad multipliceras med ett tal t multipliceras determinanten med t. Se detta med symboler!
  5. Om två rader är lika är determinanten  = 0. Se detta med symboler!
Ett lite mer överraskande för hållande är att, om man använder raderna i en determinant för att bilda en ny determinant med dessa rader som kolonner, i tur och ordning, så har de två determinanterna samma värde. Med symboler:

a1   a2   a3
b1   b2   b3
c1   c2   c3
 = a1   b1   c1
a2   b2   c2
a3   b3   c3
 .

Man kontrollerar detta genom att med hjälp av Sarrus regel se att de båda determinaterna faktiskt har samma värde.
En konsekvens av detta är:

räknereglerna 1 - 5 ovan gäller även med ordet "rad" utbytt mot "kolonn".

 
En vanlig teknik för att beräkna determinanter är att med hjälp av räknereglerna  1 - 5  omvandla determinanten till en övre trekantsdeterminat, d.v.s en av formen

a1   b1   c1
 0   b2   c2
 0    0   c3

Enligt Sarrus regel har en sådan determinant värdet  a1b2c3 .
 

Exempel 4.3.5
 
Beräkna determinanten
        D =   2    1    2
-4    3    0
 0   -4   -1
Vi multiplicerar den översta raden med  2  och adderar till den andra raden för att bli av med  -4  i den raden:
        D =  2     1    2
0     5    4
0   -4   -1
Vi adderar den tredje raden till den andra:
        D =  2     1    2
0     1   -3
0   -4   -1
Vi multiplicerar den andra raden med  4  och lägger resultatet till den tredje raden:
        D =  2   1      2
0   1     -3
0   0   -13 		= -26

 
Testövning 4.3.2
 
a) Beräkna determinanten
          1     2    3
-2     3    1
  1   -2   -1 		 .
Svar:    
b) För hur många värden på  x  är volymen på den parallellepiped som spänns av vektorerna  ( x - 1, -1, 5) ,  ( 1, x, -2)  och  ( 3, 1, x - 1)  noll? (Svara med en siffra som anger antalet eller med "oandligt" för oändligt många)
Svar:    
De är (svara med dem i storlektsordning, med det minsta först)
   x =   ,   och  .  
c) Visa att

1   a   a2
1   b   b2
1   c   c2 		 . = ( b - a)( c - a)( c - b)

Hjälp

Exempel 4.3.6
 
Beräkna volymen av den parallellepiped som spänns av vektorerna  u = ( 2, -1, 1) ,  v = ( 2, 2, 1)  och  w = ( 1, 1, -2).
 
Volymen ges av absloutbeloppet av talet  u · ( vw) , eller, med andra beteckningar, av  det( u, v, w).
Vi ska alltså beräkna absolutbeloppet av talet
          1    1  -2
2   -1  1
2    2  1
  .
Det spelar här inge roll hur på vilken rad vi placerar de olika vektorerna, eftersom olika placeraringa bara påverkar determinantens tecken och vi ska ju ändå beräkna absolutbeloppet av determinten.
Vi kan nu välja mellan en rad olika strategier för att beräkna determinanten. Vi ska försöka överföra den på övre trekantsform och har därför valt att sätta den vektor med  1  som första koordinat på översta raden. Men det finns alltså flera möjliga alternativa stategier för beräkning.
Vi multiplicerar den översta raden med  -2  och adderar resultatet till de två övriga raderna. Vi får då att dererminanten blir
          1    1  -2
0   -3  5
0    0  -4
   = 1·(-3)(-4) = 12,
vars absolutbelopp är  12. Volymen blir alltså  12.

 
Exempel 4.3.7
 
För vilka värden på  a  ligger de tre vektorerna  u = ( a, 1, 1) ,  v = ( 2, 1, a)  och  w = ( 2, 1, 1) i ett och samma plan?
 
De tre vektorerna ligger i ett och samma plan precis när volymnen av den parallellepiped som de spänner ut är noll, d.v.s när  det( u, v, w) = 0.
Vi ska alltså avgöra för vilka värden på  a  som determinanten
        a   1   1
2   1   a
2   1   1
  
är noll.
För att beräkna determinanten använder vi först räkneregler för att förenkla den. Vi multiplicerar den andra kolonnen med  -a  och  -1  och adderar resultaten till den första respektive tredje kolonnen. Determinanten blir då
        0        1        0
2 - a   1   a - 1
2 - a   1        0
 .
Vi bryter ut  2 - a  och  a - 1  ur första respektive tredje kolonnen och få att determinanten blir
        ( 2 - a)( a - 1) 0   1   0
1   1   1
1   1   0
 .
Med Sarrus regel blir determinaten nu

( 2 - a)( a - 1)·1,

så att de tre vektorena  u, v  och  w  ligger i ett och samma plan precis när  a = 2  eller  a = 1.


 
Exempel 4.3.8
 
Bestäm en ekvation på normalform för det plan som går genom  ( 2, -1, 1)  och har riktningsvektorerna  ( 2, 1, 2) och  ( 1, -1, 3).
 
En punkt ( x, y, z) ligger i planet precis när vektorn  ( x - 2, y + 1, z - 1)  ligger i samma plan som de två riktningsvektorerna. Detta inträffar precis när
        x - 2   y + 1   z - 1
     2          1        2
     1         -1       3 		= 0.
vilket är ett sätt att ange planets ekvation på normalform.

Testövning 4.3.3
 
a) Går det att bestämma talet  a  så att volymen av parallellepipeden som spänns av de tre vektorerna  ( 1, 1, a),   ( 1, 2, -1)   ( 1, 4, 1) är  10 ?
 
Ja
Nej
 
Vad ska  a  vara?
 
Svar:    a =    eller    

 
b) Låt  u  och  v  vara vektorer i rummet. Visa att de tre vektorerna  u,   v  och  u( uv)  ligger i ett och samma plan.
 
Hjälp
 
c) Ekvationen
        x - 1   y - 1   z - 2
     1         2        3
     2         5        6 		= 0
är ekvationen för ett plan genom punkten  ( 1, 1, 2) . Förklara varför Du utan nämvärt räknande kan se att linje  ( 3, t, 8)  löper i detta plan.
 
Hjälp