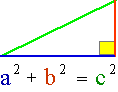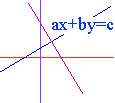ANALYTISK GEOMETRI
MED TILLÄMPNINGAR
START
KAPITEL 1
FÖRELÄSNINGAR
LEKTIONER
ÖVNINGAR
KAPITEL 2
FÖRELÄSNINGAR
LEKTIONER
ÖVNINGAR
KAPITEL 3
FÖRELÄSNINGAR
LEKTIONER
ÖVNINGAR
KAPITEL 4
FÖRELÄSNINGAR
LEKTIONER
ÖVNINGAR
KAPITEL 5
FÖRELÄSNINGAR
LEKTIONER
ÖVNINGAR
Instruktioner
För muspekaren över kompassen till vänster. När Du inte kan komma
längre kan Du klicka för att öppna det avsnitt Du pekar på
Innehåll
- Analytisk geometri i planet
- Vektorer och koordinater
- Projektioner och avstånd
- Areor och volymer
- Matristransformationer
- Koordinater och avstånd
- Räta linjer i planet
- Cirklar och vinklar
- Trigonometriska funktioner
- Transformationer
- Vektorer
- Vinklar mellan vektorer
- Tillämpningar
Koordinater och avstånd
I detta avsnitt skall vi beskriva hur man kan representera punkter i
ett plan med par av reella tal, dvs med punktens koordinater. Vi
skall också diskutera hur man med hjälp av Pythagoras sats kan finna
avståndet mellan två punkter.
Avsnittets underrubriker är:
- Talaxeln
- Avstånd och absolutbeloppet
- Koordinatssystem i planet
- Avstånd till origo
- Avstånd mellan godtyckliga punkter
Räta linjer i planet
Givet två olika punkter i planet så finns alltid precis en linje (en
entydigt bestämd linje) som går igenom dessa punkter. Den kortaste
vägen mellan de två punkterna följer ett stycke av denna rät linje.
Detta förhållande är en viktig anledning till att man intresserar sig
för
räta linjer. Varje rät linje kan beskrivas med hjälp av en ekvation av
formen
Avsnittets underrubriker är:
- Klassificering av linjer
- Linjer med positiv lutning
- Linjer med negativ lutning
- Linjens ekvation på formen ax + by = c
- Skärningspunkt mellan två linjer
Cirklar och vinklar
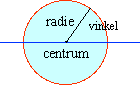
Vi skall här beskriva hur man mäter vinklar och hur man kan beskriva
cirklar i planet med hjälp av ekvationer. Vi skall också studera
eventuella skärningspunkter mellan cirklar och linjer och kommer i det
sammanhanget in på lösning av andragradsekvationer.
Avsnittet har följande underrubriker:
- Cirkelns ekvation
- Enhetscirkeln
- Vinklar och vinkelmått
- Skärningspunkter mellan linjer och cirklar
- Tangent till en cirkel
- Andragradsekvationer
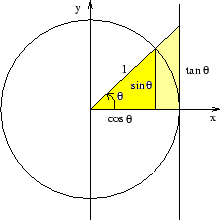
Trigonometriska funktioner
Huvudrubriker:
- Cosinus och sinusfunktionerna
- Tangensfunktionen
- Utvidgning av definitionerna
- Enkla samband
- Additionsformler
- Polär representation
Transformationer
Ordet
transformation betyder omformning, förvandling. Man kan exempelvis
tranformera en geometrisk figur genom att flytta den, rotera den kring
en punkt, spegla den i en linje, trycka ihop den osv. En transformation
kan påverka planets alla punkter eller bara punkterna i en viss delmängd
av planet. I matematiska sammanhang har begreppet transformation samma
betydelse som
avbildning eller
funktion. Man vill använda olika ord för samma sak för att därmed antyda nyanser i hur man tänker. Säger man transformation så tänker man på att något förändras. Avbildning är en mera statisk representation av något, ungefär som ett fotografi eller en kartbild. Ordet funktion antyder beroende, orsak och verkan.
- Vad är en transformation
- Exempel : Parallellförflyttning
- Sammansättning av parallellförflyttningar
- Generella translationer
- Rotation kring origo
- Speglingar i axlarna
Vektorer
Vektorbegreppet är mycket viktigt i geometrisammanhang, men det har också viktiga tillämpningar inom fysik till exempel för att analysera krafter. Vi definierar här vektorer med hjälp av translationer och beskriver hur man kan räkna med vektorer. Som en tillämpning diskuterar vi en alternativ beskrivning av räta linjer.
Definition av begreppet vektor
Räkning med vektorer
Linjens ekvation i parameterform
Diskussion om valfrihet
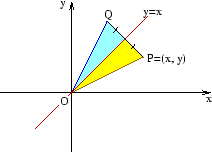
Vinklar mellan vektorer
I detta avsnitt fortsätter vi att arbeta med vektorer. Först skall vi definiera längden av en vektor och vinkeln mellan två vektorer. Sedan skall diskutera vinkelräta vektorer och det närbesläktade begreppet ortogonala vektorer. Dessa begrepp skall vi sedan använda för att visa hur man finna den så kallade normalen till en linje. Med hjälp av den skall vi återvända till räta linjer och deras ekvationer.
- Längd av vektor
- Vinkeln mellan två vektorer
- Ortogonala vektorer
- Olika beskrivningar av en rät linje
Tillämpningar
I detta avsnitt ger vi några tillämpningar och utvidgningar av föregående avsnitt. Avsnittets huvudrubriker är:
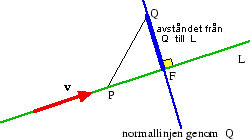
- Ortogonal projektion på en linje
- Avstånd från en punkt till en linje
- Spegling i en linje
- Cosinussatsen
- Sinussatsen, avståndsmätning
- Koordinatsystem i planet och rummet (introduktion)
- Vektorer i planet och i rummet
- Linjer och plan
- Skalärprodukt
- Beräkning av vinklar