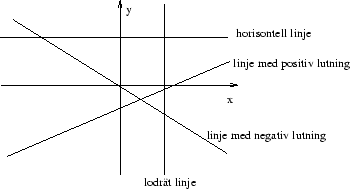
Lutande linjer kan beskrivas med ekvationer av typ
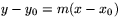 eller
eller 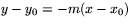 . Sätter vi
. Sätter vi 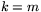 eller
eller
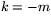 kan vi nu beskriva varje lutande linje med en ekvation av formen
kan vi nu beskriva varje lutande linje med en ekvation av formen
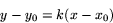
Här är 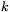 positiv om linjen har positiv lutning (
positiv om linjen har positiv lutning (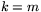 ) och
) och 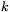 är
negativ (
är
negativ (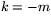 ) om lutningen är negativ.
) om lutningen är negativ.
Vi påstår nu att en godtycklig linje som går genom punkten
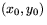 kan kan skrivas på
formen
kan kan skrivas på
formen
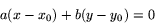
där 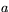 och
och 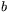 inte båda är noll. Tar man nämligen
inte båda är noll. Tar man nämligen 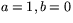 så
får vi ekvationen
så
får vi ekvationen 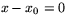 för en lodrät linje. Tar vi istället
för en lodrät linje. Tar vi istället 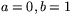 så får vi den vågräta linjen
så får vi den vågräta linjen 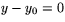 . Väljer vi däremot
. Väljer vi däremot 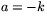 och
och
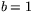 så ger ekvationen ovan sambandet för en lutande linje.
så ger ekvationen ovan sambandet för en lutande linje.
Vänster led i ekvationen ovan kan vi skrivas som
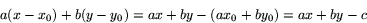
där
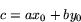
Flyttar vi över 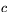 på höger sida får vi den generella ekvationen
på höger sida får vi den generella ekvationen
Vi har nu kommit fram till att varje linje kan beskrivas med en ekvation
av denna form.
 Exempel D
Exempel D
 Exempel E
Exempel E
 Exempel F
Exempel F
 Testövning
Testövning
Exempel D
Ekvationen 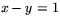 beskriver den räta linje som går igenom origo och
punkten
beskriver den räta linje som går igenom origo och
punkten 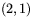 .
.
Samma linje kan också beskrivas med ekvationen
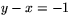 eller med
eller med 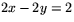 .
Exempel E
.
Exempel E
Bestäm en ekvation för linjen genom två punkter på
koordinataxlarna.
Låt punkterna vara 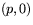 och
och 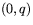 och antag att
och antag att 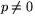 .
.
Visa lösningen
Exempel F
Sök en ekvation för den linje som går igenom 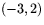 och
och
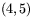 .
.
Visa lösning
Testövning
Sök en ekvation för den linje som går igenom (5,9) och
(0,6)!
Mata in koefficienterna!
![]() -axelns ekvation ut?
-axelns ekvation ut?