I detta avsnitt kommer vi så småningom fram till att alla linjer kan beskrivas med en enda sorts ekvation.
 

 Ekvationen för en vågrät linje är

där är en konstant. Ekvationen för en lodrät linje är

där är en konstant.
Ekvationen för en linje med positiv lutning :

där är positiv () och och är konstanter. Ekvationen för en linje med negativ lutning :

där är negativ () och och är konstanter. Rätt!
Ekvationen för -axeln är Det var inte rätt! Försök igen!




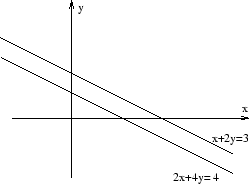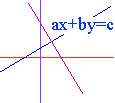
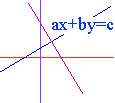
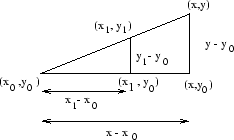
Den större triangeln med hörn i punkterna , och är likformig med den mindre triangeln, vars hörn ligger i punkterna , och . Detta innebär att den större triangeln kan ses som en förstoring av den mindre i en viss skala. Därför är förhållandena mellan trianglarnas katetrar en konstant. Vi har alltså

där är en konstant.
I figuren ovan har vi antagit att . Att linjen har en positiv lutning innebär att man i så fall också har att . Därför måste konstanten vara positiv. Vi har alltså att

om . Du kan övertyga dig om att samma formel även gäller då . (Se kompendiet!)
Alldeles riktigt. Linjen genom origo och punkten har ekvationen .
Låt oss generalisera (utvidga) frågan!

Vilken linje genom origo går också genom punkten som ligger i första kvadranten?

Visa svaret

Om en linje går origo har den ekvationen . För att linjen också skall passera måste , vilket ger . Linjens ekvation är alltså

eller om man vill

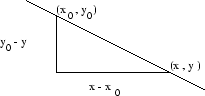
Linjens ekvation måste vara av formen . Vilket värde måste ha om skall ligga på linjen?

 





Riktigt! Linjen genom punkterna och har ekvationen det vill säga . Man kan också skriva ekvationen på formen

Bestäm ekvationen för linjen genom punkterna och där är ett positiva tal!

Visa svaret

Ekvationen är

Man kan naturligtvis också skriva (exemeplvis). Svaret skall ha formen . Försök igen!

Först sätter vi upp linjens ekvation:

Träffpunkten med linjen måste ha en -koordinat som uppfyller sambandet

Detta ger . Träffpunkten är alltså . Detta är alltså skärningspunkten mellan de båda givna linjerna. Exempel E Lösning
Vi söker ekvationen för linjen genom och .

Linjen måste ha en ekvation av formen , eftersom linjen går genom . För att linjen dessutom skall gå genom måste vi ha , dvs . Vi får alltså ekvationen

Man kan också skriva linjens ekvation så här:

Exempel F Lösning
Vi söker en ekvation för den linje som går igenom och .

Om linjen har ekvationen måste satisfiera ekvationen, vilket ger . Vidare måste punkten uppfylla villkoret . Detta ger

Låt oss ta . Då får vi och . Detta ger ekvationen

Vad händer om man väljer ett annat värde på a ?

Tag vilket -värde som helst (utom noll). Då får man och . Linjens ekvation blir då

Här är en gemensam faktor i alla tre termerna, så vi kan dividera bort . Vi får då ekvationen

Efter multiplikation av båda leden med återfår vi samma ekvation som vi fick ovan.

Exempel G
En linje har ekvationen . Var skär linjen koordinataxlarna?




Visa hur man bestämmer skärningspunkterna!

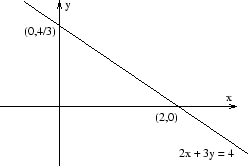
För att svara på frågan tänker vi oss att skärningspunkten med -axeln har koordinaterna . Ekvationen ger då att dvs , . Skärningspunkten med -axeln är således .

På samma sätt måste skärningspunkten med -axeln uppfylla villkoret , vilket ger skärningspunkten .

Exempel H
Låt två linjer och vara givna med sina ekvationer:

Vi söker skärningspunkten (om det finns någon).

Visa lösningen

Om det finns en skärningspunkt måste dess koordinater uppfylla båda villkoren (båda ekvationerna). Vi markerar det genom att skriva en klammer om ekvationerna:

Detta är ett ekvationssystem. Vi söker nu tal och som uppfyller båda ekvationerna i systemet.

Beräkna skärningspunkten!

Visa figur!

För att finna och multiplicerar vi den första ekvationen med och adderar till den andra. Vi får då att , vilket ger . Vi har då det förenklade systemet

Detta ger och . Skärningspunkten är därför .




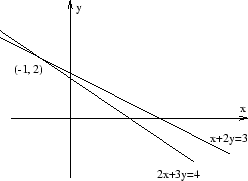
Figuren visar de båda linjerna

Exempel I
Vi betraktar här linjerna och vara givna med ekvationerna:

Liksom i föregående exempel multiplicerar vi den första ekvationen med och adderar till den andra. Vi får då vilket ger det chockerande beskedet . Detta är orimligt. Förklaringen är att de givna linjerna är parallella.