En cirkel bestäms av sin medelpunkt (eller centrum) och sin radie. Cirkeln består av alla punkter vars avstånd till medelpunkten är lika med dess radie. Låt cirkelns medelpunkt vara 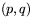 och radien vara
och radien vara 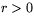 . Avståndet från en punkt
. Avståndet från en punkt 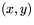 på cirkeln till medelpunkten är då
på cirkeln till medelpunkten är då
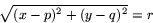
Kvadrerar vi detta samband får vi
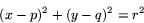
Detta kallar vi ekvationen för cirkeln med centrum i 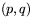 och radien
och radien 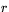 . Ekvationen beskriver alla punkter som ligger på cirkeln, genom att ge ett villkor som punkternas koordinater måste uppfylla. Med hjälp av cirkelns ekvation kan man avgöra om en given punkt ligger på en cirkel med given medelpunkt och given radie.
. Ekvationen beskriver alla punkter som ligger på cirkeln, genom att ge ett villkor som punkternas koordinater måste uppfylla. Med hjälp av cirkelns ekvation kan man avgöra om en given punkt ligger på en cirkel med given medelpunkt och given radie.
Exempel A
Exempel B
 Exempel C
Exempel C
 Exempel D
Exempel D
Exempel C
Se på ekvationen
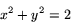
Detta är ekvationen för en cirkel med centrum i origo!
Vilken är cirkelns radie?
Tips för inmatning av tal
Exempel D
Betrakta ekvationen
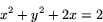
Detta är en ekvation för en cirkel. Vilken?
Visa lösningen
Ett viktigt specialfall är cirklar med centrum i origo. Då är 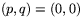 dvs
dvs 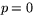 och
och 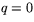 . Ekvationen (1) får då formen
. Ekvationen (1) får då formen 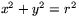 . Om
. Om 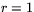 har vi den så kallade enhetscirkeln vars ekvation alltså är
har vi den så kallade enhetscirkeln vars ekvation alltså är
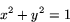
Enhetscirkeln är således cirkeln med centrum i origo och radien  .
.
Exempel E
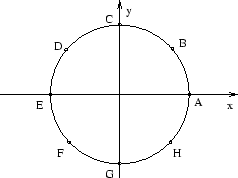
Figuren visar enhetscirkeln! De utmärkta åtta punkterna är skärningspunkterna mellan enhetscirkeln och koordinataxlarna och de båda linjerna 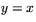 och
och 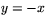 . Vilka är koordinaterna för de åtta punkterna?
. Vilka är koordinaterna för de åtta punkterna?
Visa
Låt 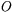 beteckna origo och låt
beteckna origo och låt 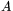 och
och 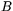 vara två punkter på enhetscirkeln. Linjestyckena (sträckorna)
vara två punkter på enhetscirkeln. Linjestyckena (sträckorna) 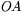 och
och  bildar då en vinkel. I figuren har vi valt
bildar då en vinkel. I figuren har vi valt  . man kan tänka sig att sträckan
. man kan tänka sig att sträckan  är visaren på en klocka, men i matematiska sammanhang brukar man vanligen låta klockan gå åt fel håll jämfört med våra vanliga klockor med visare.
är visaren på en klocka, men i matematiska sammanhang brukar man vanligen låta klockan gå åt fel håll jämfört med våra vanliga klockor med visare.
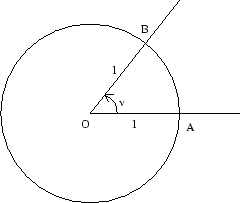
Det finns många sätt att mäta vinklar. Alla går i princip ut på att man tilldelar hela varvet ett visst mått. Som mått på en vinkel anger man antalet delar av hela varvet som vinkeln upptar. Ett vanligt mått är gradmåttet. Man delar då upp hela varvet i 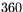 grader. Beteckningen för gradmåttet är
grader. Beteckningen för gradmåttet är 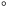 . Ett helt varv upptar alltså
. Ett helt varv upptar alltså 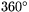 . Gradmåttet av en vinkel är antalet grader eller delar av grader som vinkeln upptar.
. Gradmåttet av en vinkel är antalet grader eller delar av grader som vinkeln upptar.
I matematik är det vanligaste vinkelmåttet radianer. Här tilldelar man hela varvet måttet  , vilket är längden av enhetscirkeln, alltså dess omkrets. Mätetalet för en vinkel blir då lika med längden av cirkelbågen från
, vilket är längden av enhetscirkeln, alltså dess omkrets. Mätetalet för en vinkel blir då lika med längden av cirkelbågen från 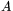 till
till 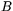 . (Kom ihåg att
. (Kom ihåg att 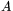 och
och 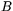 är punkter på enhetscirkeln.) Vi kommer inte att använda någon speciell beteckning för vinkelmått i radianer.
är punkter på enhetscirkeln.) Vi kommer inte att använda någon speciell beteckning för vinkelmått i radianer.

Exempel F
Samband mellan grader och radianer
Sambandet mellan vinkelmått i radianer och i grader är enkelt. Eftersom gradmåttet anger hur många delar av 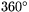 som vinkeln upptar får man
som vinkeln upptar får man
Detta är detsamma som att
För exempel på omvandlingar mellan grader och radianer klicka
här
En given linje kan skära en given cirkel i en eller högst två punkter. Eventuellt kan skärningspunkt saknas.
Exempel G
Vi skall undersöka skärningspunkterna mellan enhetscirkeln och linjen  . Eventuella skärningspunkter
. Eventuella skärningspunkter 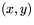 måste uppfylla både cirkelns och linjens ekvation, dvs
måste uppfylla både cirkelns och linjens ekvation, dvs 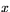 och
och 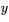 måste lösa ekvationssystemet
måste lösa ekvationssystemet
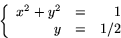
Visa lösningen
Exempel H
Definition
Låt 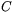 vara en cirkel. En linje kallas en tangent till cirkeln
vara en cirkel. En linje kallas en tangent till cirkeln 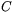 om linjen och cirkeln har precis en skärningspunkt (precis en gemensam punkt).
om linjen och cirkeln har precis en skärningspunkt (precis en gemensam punkt).
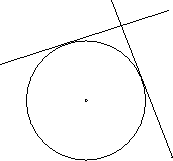
Figuren beskriver en cirkel och de två tangenter som kan dras från en punkt utanför cirkeln.
Exempel I
Exempel J
Vi har ovan gått igenom några exempel där vi sökt eventuella skärningspunkter mellan en cirkel och en linje. Detta har lett till ekvationer av typen
Detta är ett exempel på en andragradsekvation.
Det finns tre fall
Problemet att finna eventuella skärningspunkter mellan en cirkel och en linje leder ibland till mer komplicerade andragradsekvationer, nämligen ekvationer av typen
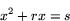 där
där 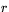 och
och  är givna tal.
är givna tal.
Lösningarna till ekvationen 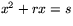 ser ut så här:
ser ut så här:
Fall 1: 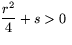 .
Lösningarna är
.
Lösningarna är
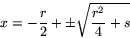 Fall 2:
Fall 2: 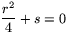 .
Lösningarna är
.
Lösningarna är
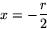 Fall 3:
Fall 3: 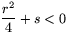 . Lösningar saknas!
. Lösningar saknas!
Visa härledningen av dessa formler
 Exempel K
Exempel K
 Exempel L
Exempel L
Exempel K
Lös följande tre andragradsekvationer:
(a) 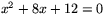 Visa
Visa
(b) 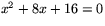 Visa
Visa
(c) 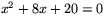 Visa
Visa
Exempel L
Sök eventuella skärningspunkter mellan 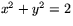 och
och 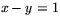 .
.
Visa
![]() och radien vara
och radien vara ![]() . Avståndet från en punkt
. Avståndet från en punkt ![]() på cirkeln till medelpunkten är då
på cirkeln till medelpunkten är då
![]()
![]()
![]()
![]()