cos, sin, tan .
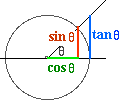

Koordinaterna ![]() och
och ![]() för punkten
för punkten ![]() måste vara bero på
måste vara bero på ![]() . De måste med andra ord vara funktioner av
. De måste med andra ord vara funktioner av ![]() . Dessa funktioner är de två trigonometriska grundfunktionerna cosinus och sinus. Vi skriver
. Dessa funktioner är de två trigonometriska grundfunktionerna cosinus och sinus. Vi skriver
![]()
Eftersom ![]() är en punkt på enhetscirkeln så gäller
är en punkt på enhetscirkeln så gäller
![]() . Ofta skriver man
. Ofta skriver man ![]() i stället för
i stället för ![]() och motsvarande för sinusfunktionen. Vi har alltså
och motsvarande för sinusfunktionen. Vi har alltså
![]()
Formeln brukar kallas ``den trigonometriska ettan''.
(a) Om ![]() är
är ![]() . Alltså gäller
. Alltså gäller
![]()
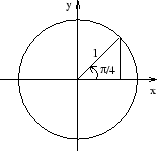
(b) Om ![]() är
är ![]() . Alltså gäller
. Alltså gäller
![]()
(c) Om ![]() är
är ![]() . Alltså gäller
. Alltså gäller
![]()
(d) Vinkeln i en liksidig triangel är ![]() .
.
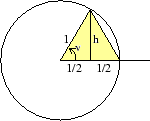
I figuren är ![]() . Detta visar att om
. Detta visar att om ![]() är
är ![]() .
Alltså gäller
.
Alltså gäller
![]()
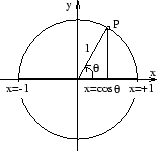
Av figuren ser man att man kan välja ![]() i intervallet
i intervallet
![]() .
.
Talet ![]() skrivs här pi.
skrivs här pi.
Kvadratroten ur ett tal x skrivs sqrt(x)
De elementära räknesätten skrivs + - * /
Man måste skriva ut gångertecknet *
![]()
Däremot är tangensfunktionen inte definierad för ![]() , eftersom
, eftersom ![]() .
.
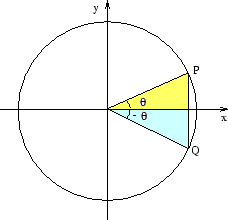
I figuren är ![]() och
och ![]() . Eftersom
. Eftersom ![]() och
och ![]() har samma
har samma ![]() -koordinat följer det att
-koordinat följer det att ![]() . Å andra sidan har punkternas
. Å andra sidan har punkternas ![]() - koordinater olika tecken, vilket ger
- koordinater olika tecken, vilket ger ![]() .
.
Exempel
Exempel K
Dessutom har vi att
Med hjälp av en kalkylator får man att
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Med hjälp av additionsformeln för cosinusfunktionen kan man beräkna ![]() om man känner
om man känner ![]() . Vi har nämligen att
. Vi har nämligen att
![]()
![]() och får då att
och får då att
![]()
![]() (eller snarare
(eller snarare ![]() ) med denna formel. Man får som synes att
) med denna formel. Man får som synes att
![]()
![]()
Med hjälp av additionsformeln för sinus fär vi att
![]()
![]()
Sätt ![]() . Då är
. Då är ![]() . Eftersom
. Eftersom
![]()
![]() den polära framställningen
den polära framställningen
![]()
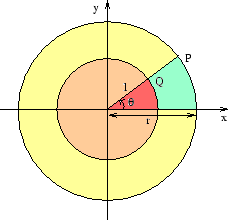
Vi kan tänka oss att triangelns hörn vid vinkeln ![]() ligger i origo och att motsvarande kateter fallar utmed
ligger i origo och att motsvarande kateter fallar utmed ![]() -axeln. Det andra hörnet som står mot den räta vinkeln har då koordinaterna
-axeln. Det andra hörnet som står mot den räta vinkeln har då koordinaterna ![]() , där
, där ![]() och
och ![]() är katetrarnas längder. Eftersom avståndet till origo är längden av hypotenusan (alltså
är katetrarnas längder. Eftersom avståndet till origo är längden av hypotenusan (alltså ![]() ) så får vi att
) så får vi att
![]()
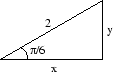
Om den vinkel som står mot den kortare katetern är ![]() så gäller
så gäller
![]()
![]() . Nu är inte 2/3 tangens för en vinkel som vi redan har beräknat. I detta läge får man ta till en
kalkylator
. Nu är inte 2/3 tangens för en vinkel som vi redan har beräknat. I detta läge får man ta till en
kalkylator
![]()
En enkel manual till räknedosan finns
här
Knappen Rensa tömmer båda fönstren.
Knappen = gör att beräkningen utförs
Knappen x= gör att det beräknade värdet sparas med symbolen x
Knappen x tar fram värdet på x
Knappen y= gör att det beräknade värdet sparas med symbolen y
Knappen y tar fram värdet på y
Knappen asin: asin(t) ger den vinkeln mellan -pi/2 och pi/2 vars sinus är t
Knappen acos: acos(t) ger den vinkeln mellan 0 och pi vars cosinus är t
Knappen atan: atan(t) ger den vinkeln mellan -pi/2 och pi/2 vars tangens är t
Övriga knappar är förhoppningsvis självinstruerande!
Om du får texten "undefined" har du förmodligen försökt mata in något
i det undre fönstret--det är bara avsett för att visa resultat.
Om allt försvinner har du antagligen tryck på knappen Rensa i stället
för =
Om du får texten "Formelfel!" så har du gjort något galet i
inmatningen--exempelvis glömt * eller parenteser.
Om inget händer eller det står javascript error i nedersta raden i
kalkylatorns fönster har du hittat ett programfel. Känn dig stolt!