Om 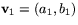 och
och 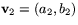 är två vektorer så
definierar vi deras summa
är två vektorer så
definierar vi deras summa 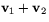 genom att sätta
genom att sätta
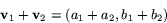
Man bör här jämföra med sammansättning av translationer.

Vi definierar också multiplikation mellan ett tal och en vektor på
följande sätt. Låt 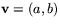 vara en vektor och
vara en vektor och 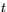 ett tal. Vi
definierar då
ett tal. Vi
definierar då 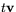 genom att sätta
genom att sätta
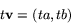

Slutligen definierar vi subtraktion mellan vektorer på följande sätt. Om
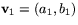 och
och 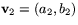 så sätter vi
så sätter vi
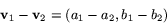

Exempel C
 Exempel D
Exempel D
Exempel D
Börja med att rita ut punkterna (1,4) och (3,-2) i ett rätvinkligt koordinatsystem. Rita sedan ut mittpunkten på sträckan mellan dessa punkter. Vilka koordinater har mittpunkten?
Hur tror du att man kan bestämma mittpunktens koordinater genom att bara räkna med koodinater?
Visa ett tips
Vi har tidigare beskrivit linjer med hjälp av ekvationer av formen
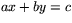 . Det finns en annan naturlig beskrivning av linjer. Man tänker
sig linjen (eller ett stycke av linjen) som bana för en partikel som
passerar en viss punkt
. Det finns en annan naturlig beskrivning av linjer. Man tänker
sig linjen (eller ett stycke av linjen) som bana för en partikel som
passerar en viss punkt 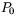 vid ett visst ögonblick och rusar i väg med
en viss hastighet
vid ett visst ögonblick och rusar i väg med
en viss hastighet 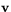 . Hastigheten är här en vektor som anger både i
vilken riktning partikeln far och hur fort den rör sig. En punkt på
linjen kan då beskrivas genom att man talar om vid vilken tidpunkt som
punkten passeras. Låt oss säga att den fixa punkten
. Hastigheten är här en vektor som anger både i
vilken riktning partikeln far och hur fort den rör sig. En punkt på
linjen kan då beskrivas genom att man talar om vid vilken tidpunkt som
punkten passeras. Låt oss säga att den fixa punkten 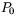 passeras vid tiden
passeras vid tiden
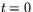 . Om
. Om 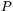 är en godtycklig punkt på linjen som passeras vi
tidpunkten
är en godtycklig punkt på linjen som passeras vi
tidpunkten 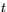 , så gäller
, så gäller
Detta kallas linjens ekvation i parameterform.

Man kan skriva ut vad den inramade ekvationen innebär för koordinaterna för 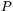 .
Om
.
Om 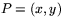 ,
, 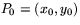 och
och 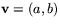 så är
så är
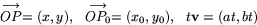
Höger led är därför
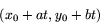
Därför kan linjens ekvation i parameterform skrivas som
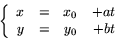
Här måste vi naturligtvis anta att åtminstone ett av talen 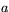 eller
eller 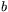 är skiljt från noll (
är skiljt från noll (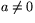 eller
eller 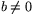 ).
).
Exempel E
Exempel F
 Exempel G
Exempel H
Exempel G
Exempel H
Exempel G
En linje har ekvationen 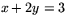 . Beskriv denna linje i parameterform.
. Beskriv denna linje i parameterform.
Ledning: Två saker behövs, nämligen
-
en punkt på linjen
-
en riktningsvektor.
Tänk efter hur man skall en punkt på linjen och sedan en riktningsvektor!
Visa!
Exempel H
Bestäm en punkt på linjen 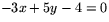 .
.
Bestäm sedan en riktningsvektor!
När du har kommit fram till ett svar
klicka här
![]() Exempel B
Exempel B
![]() och
och ![]() . Bestäm
. Bestäm ![]() .Svar:
.Svar: