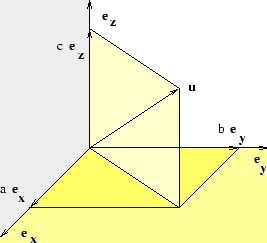

Antag att ![]() . Det gäller att visa att
. Det gäller att visa att ![]() ,
, ![]() och
och ![]() .
.
Eftersom ![]() kommer
kommer ![]() att translateras till
att translateras till ![]() Alltså måste
Alltså måste![]()
Men detta ger just att ![]() ,
,![]() och
och ![]() . Beviset är klart!
. Beviset är klart! ![]()
I resonemanget ovan har vi arbetat i rummet ![]() . Motsvarande resultat i planet
. Motsvarande resultat i planet ![]() får man genom att bortse från
tredjekoordinaterna.
får man genom att bortse från
tredjekoordinaterna.
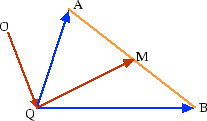
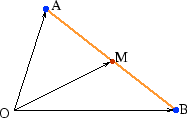
I figuren visas en vektor ![]() i planet och två punkter
i planet och två punkter ![]() och
och ![]() . Vi söker koordinaterna för
. Vi söker koordinaterna för ![]() om
om ![]()
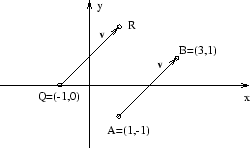
Vi får ![]() . Eftersom
. Eftersom ![]() drar vi slutsatsen att
drar vi slutsatsen att ![]() .
.
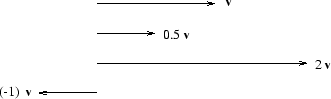
alltså att
Observera att varje vektor är parallell med nollvektorn!
För varje vektor u gäller ju att ![]() .
.
![]()
![]()
![]()
![]()
Anmärkning
![]() . Motsvarande definitioner i planet
. Motsvarande definitioner i planet ![]() får man genom att bortse från tredje-koordinaterna. Om alltså
får man genom att bortse från tredje-koordinaterna. Om alltså ![]() och
och ![]() så är exempelvis
så är exempelvis ![]() . Nollvektorn i planet är
. Nollvektorn i planet är ![]() . På samma sätt blir
. På samma sätt blir ![]()
![]()
Men
![]()

Men
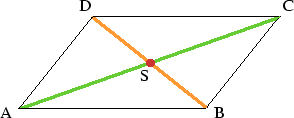
För att visa detta låter vi ![]() vara mittpunkt på diagonalen
vara mittpunkt på diagonalen ![]() . Vi vill visa att
. Vi vill visa att ![]() också ligger på diagonalen
också ligger på diagonalen ![]() , ja till och med att
, ja till och med att ![]() är mittpunkt på
är mittpunkt på ![]() . Enligt föregående exempel är
. Enligt föregående exempel är
![]()
![]()
![]()
Räknelagarna (5) och (6) brukar kallas distributiva lagar.
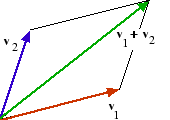
Den kommutativa lagen (1) utsäger att ordningen inte spelar någon roll vid vektoraddition. För att förstå den associativa lagen (2) måste man vara medveten om den i matematiken ofta använda parenteskonventionen: operationer som står inom parentes skall utföras först. Den associativa lagen (2) innebär alltså att om man först adderar ![]() och
och ![]() och därefter lägger till
och därefter lägger till ![]() , så kommer man att få samma resultat som man får om man adderar
, så kommer man att få samma resultat som man får om man adderar ![]() till summan av
till summan av ![]() och
och ![]() . Tre vektorer kan därför summeras i vilken ordning som helst. Räknelagarna (3) och (8) är ju naturliga -- om man adderar nollvektorn till en vektor eller multiplicerar den med talet 1 så ändras inte vektorn. Räknelagen (4) kan ges en generellare form om man vill:
. Tre vektorer kan därför summeras i vilken ordning som helst. Räknelagarna (3) och (8) är ju naturliga -- om man adderar nollvektorn till en vektor eller multiplicerar den med talet 1 så ändras inte vektorn. Räknelagen (4) kan ges en generellare form om man vill:![]()
De båda distributiva lagarna talar om hur man får blanda multiplikation och addition och manipulera parenteser.
Det finns flera andra räknelagar som man kan ha nytta av, till exempel![]()
Bevisen av de åtta räknelagarna använder sig av definitionerna av addition och multiplikation med tal samt motsvarande räknelagar för reella tal. Vi nöjer oss med att bevisa den distributiva lagen (5) i planet ![]() . Säg alltså att
. Säg alltså att![]()
Då är ![]()
Vänster led i (5) är alltså ![]()
medan höger led är ![]()
Dessa båda led är lika eftersom ![]()
Som läsaren inser blir beviset i rummet likadant -- bara en tredje koordinat att skriva.
De övriga räknelagarna visas på ett snarlikt sätt.
och konstaterar på liknande sätt att varje vektor ![]() entydigt
kan skrivas
entydigt
kan skrivas
| (10) |