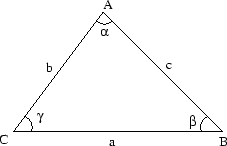
Vi börjar med ett exempel i planet. Syftet med exemplet är att påvisa sambandet mellan vinklar och skalärprodukten.
Definition 1
Låt
![]()
![]()
![]()
Exempel H (om avståndsmätning)
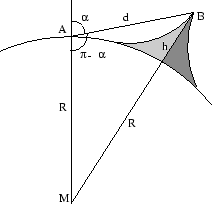
Exempel I (om höjdmätning)
Triangulering (triangelmätning) går till så att man med ett vinkelinstrument (teodolit) mäter vinklarna till ett avlägset objekt från ändpunkterna av en känd
bassträcka mäts. Sedan kan man räkna ut avståndet till objektet med hjälp av sinussatsen. Principen används inte bara av lantmätare utan även vid astronomisk
avståndsbestämning eller för att hjälpa robotar att
"se".
Vid löptidsmätning mäter man den tid det tar ljuset att färdas till
föremålet (och eventuellt tillbaka via en reflektor). Med
hjälp av den kända ljushastigheten (ca 300 m/ms) kan man sedan beräkna
avståndet. Denna princip används till exempel i
radar. Man kan också sända ut ljud (till exempel i vatten).
Interferometri används för precisionsmätningar av avstånd. För korta
distanser används laserljus. Vid längre avstånd kan
man använda radiovågor. Man jämför hur strålar som sänts via en
reflektor på objektet interfererar med direkt inkommande
strålar.
Trigonometrisk höjdmätning utnyttjas för bestämning av
höjdskillnader över stora avstånd. Exempelvis har
Mount Everests höjd mätts på detta sätt. Numera används
satellitssytemet GPS (Global Positioning System).
Man vill veta höjden över havet hos en avlägsen bergstopp. Hänsyn måste
tas till jordens krökning. Vi antar att man känner avståndet till
bergstoppen från en mätposition långt från berget. (Se föregående exempel.)
Till vårt förfogande står ett
instrument med vars hjälp man kan mäta vinkeln mellan en lodlinje och
bergets topp, så som figuren antyder. (Proportionerna är dock våldsamt
överdrivna!) För enkelhets skull har vi antagit att mätningarna sker från en punkt på havsytans nivå.
Det finns olika metoder för avståndsmätning. En av de viktigaste är
triangulering. Andra metoder är löptidsmätning och
interferometri.
Det finns många metoder för höjdmätning på jorden. En enkel men grov
metod är exemeplvis att mäta skillnader i lufttryck.