Jordklotet roterar kring en axel genom sydpolen och nordpolen. Vinkelrät mot denna axel går genom medelpunkten det så kallade ekvatorsplanet. Ett godtyckligt plan som är vinkelrät mot ekvatorsplanet och som går genom medelpunkten, skär ut en meridian. En av dessa kallas nollmeridianen. (Det är den meridian som passerar genom observatoriet i Greenwich.) Genom en given punkt på sfären går precis en meridian, vilken anger punktens longitud (eller längdgrad) i förhållande till nollmeridianen, genom att ange hur långt (mätt i grader) åt öster eller väster man måste gå. Man talar till exempel om 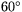 västlig längd (eller longitud
västlig längd (eller longitud 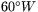 ).
).
För att ange en punkts position i förhållande till ekvatorsplanet inför man parallellcirklar. Genom en given punkt går precis en parallellcirkel, vilken anger punktens latitud (eller breddgrad) norr eller söder om ekvatorn, (mätt i grader). Parallellcirkeln på latitud 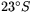 (
(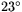 sydlig bredd) passerar till exempel (ungefär) genom Sao Paolo i Sydamerika. Detta är Stenbockens vändkrets. Motsvarande parallellcirkel på norra halvklotet kallas Kräftans vändkrets (
sydlig bredd) passerar till exempel (ungefär) genom Sao Paolo i Sydamerika. Detta är Stenbockens vändkrets. Motsvarande parallellcirkel på norra halvklotet kallas Kräftans vändkrets (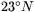 ). Den passerar strax söder om Assuan i Egypten. Vändkretsarna är de parallellcirklar, där solen står i zenit (solens strålar bildar rät vinkel mot jordytan) mitt på dagen vid resp. halvklots sommarsolstånd (den dag då solen står som högst).
). Den passerar strax söder om Assuan i Egypten. Vändkretsarna är de parallellcirklar, där solen står i zenit (solens strålar bildar rät vinkel mot jordytan) mitt på dagen vid resp. halvklots sommarsolstånd (den dag då solen står som högst).
För den matematiska behandlingen av jordytans geometri är detta
traditionella sätt att ange en orts position inte alldeles
ändamålsenligt. Man använder istället polära koordinater för att ange
positioner på sfären.
Läs mer om detta
En storcirkel på sfären är snitt mellan sfären och ett plan genom origo. Meridianerna är exempel på storcirklar. Parallellcirklar är däremot i regel inte storcirklar. Den enda parallellcirkel som är en storcirkel är ekvatorn.
Genom två olika punkter P och Q på sfären går minst en
storcirkel, nämligen den som skärs ut av planet genom origo, P
och Q. Om P och Q är antipoder, dvs
ligger på samma diameter, så finns det flera sådana storcirklar. I
annat fall finns det precis en storcirkel genom P och Q.
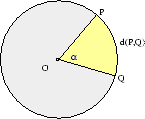
Avståndet d(P,Q) mellan P och Q är längden av den kortaste bågen på den storcirkel som sammanbinder P och Q. Det innebär detta att avståndet d(P,Q) är sfärens radie multiplicerad med vinkeln mellan vektorerna 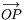 och
och 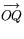 .
.

Man kan bevisa (men det ligger en bit utanför denna kurs) att en godtycklig kurva som sammanbinder två punkter P och Q och vars alla punkter ligger på sfären, måste ha en längd som är 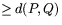 . Avståndet d(P,Q) är alltså längden av den kortaste väg som en resenär kan färdas på jordytan från P till Q.
. Avståndet d(P,Q) är alltså längden av den kortaste väg som en resenär kan färdas på jordytan från P till Q.
Ordet geodetisk kurva (eller geodetisk linje) används ofta som synonymt med ordet storcirkel på sfären. På en godtycklig yta använd ordet geodetisk kurva för kurvor av kortast möjliga längd mellan givna punkter på ytan.
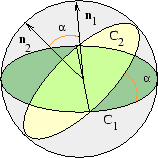
Om C1 och C2 är två geodetiska linjer på sfären så definierar vi vinkeln 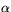 mellan dem som den Euklidiska vinkeln i
mellan dem som den Euklidiska vinkeln i 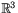 . Detta är ekvivalent med följande. Om Cj är snitt mellan sfären och planet genom origo med enhetsnormal
. Detta är ekvivalent med följande. Om Cj är snitt mellan sfären och planet genom origo med enhetsnormal 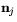 , (längden av
, (längden av 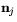 är 1) så är
är 1) så är 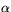 vinkeln mellan
vinkeln mellan 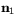 och
och 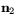 , dvs
, dvs
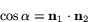
Observera att vinkeln inte är entydigt definierad med denna formel. Det finns ju två enhetsnormaler till vardera plan. Om vi emellertid kräver att vinkeln 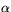 skall väljas i intervallet
skall väljas i intervallet 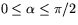 blir vinkeln entydigt definierad.
blir vinkeln entydigt definierad.
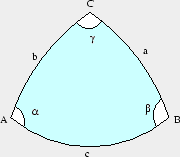
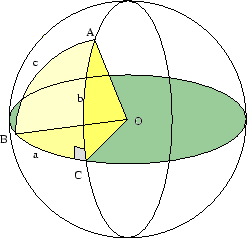
Vi kommer nu till begreppet sfärisk triangel. En sådan definieras med hjälp av tre punkter A,B,C på sfären och triangeln utgörs av dessa tre punkter samt de geodetiska bågarna mellan dem.
Man kan naturligtvis bygga upp en samling formler som beskriver samband mellan sidornas längder (dvs de geodetiska avstånden mellan triangelns hörn) och triangelns vinklar. Vi avstår från det, men ger ett exempel.
Sats (Pythagoras sats på sfären) Låt ABC vara en triangel på en sfär med radien R och med sidorna a,b resp c. Antag att vinkeln vid hörnet C är rät. Då är
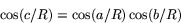
Här är således a och b katetrarna och c hypotenusan.
Läs beviset för Pythagoas sats
![]() (
(![]() sydlig bredd) passerar till exempel (ungefär) genom Sao Paolo i Sydamerika. Detta är Stenbockens vändkrets. Motsvarande parallellcirkel på norra halvklotet kallas Kräftans vändkrets (
sydlig bredd) passerar till exempel (ungefär) genom Sao Paolo i Sydamerika. Detta är Stenbockens vändkrets. Motsvarande parallellcirkel på norra halvklotet kallas Kräftans vändkrets (![]() ). Den passerar strax söder om Assuan i Egypten. Vändkretsarna är de parallellcirklar, där solen står i zenit (solens strålar bildar rät vinkel mot jordytan) mitt på dagen vid resp. halvklots sommarsolstånd (den dag då solen står som högst).
). Den passerar strax söder om Assuan i Egypten. Vändkretsarna är de parallellcirklar, där solen står i zenit (solens strålar bildar rät vinkel mot jordytan) mitt på dagen vid resp. halvklots sommarsolstånd (den dag då solen står som högst).