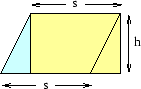
Arean av en rektangel definieras som produkten av två av rektangelns sidor som möts i ett hörn. En rätvinklig triangels area måste därför vara hälften av produkten av triangelns båda katetrar. Figuren förklarar varför.


Arean av en parallellogram måste i så fall vara produkten av en sida och en höjd mot denna sida.

I figuren har ju de båda rätvinkliga trianglarna samma katetrar och alltså samma area. Parallellogrammens area är därför lika med den markerade rektangelns area, alltså 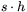. Arean av en parallellogram är alltså ``basen gånger höjden'' dvs produkten av en sida och höjden mot denna sida.


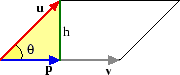
Med figurens beteckningar är parallellogrammens area alltså

(1)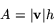
 
 

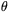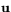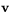Om vinkeln mellan och är känd kan man bestämma h med hjälp av formeln . Detta ger första delen av följande sats.

Sats 1
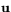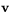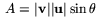Arean av en parallellogram som bestäms av vektorerna och är där 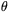är vinkeln mellan 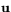och 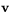. Detta innebär att
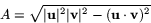
Bevis av sats 1
Exempel A
  
Låt oss använda sats 1 på en parallellogram i planet 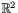. Antag att

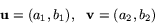
Om parallellogrammens area är A så ger sats 1 att

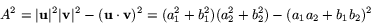
Man kan nu omforma det högra ledet och få ett enklare uttryck för arean, nämligen

A=| a1b2-a2b1 |

Visa hur denna omformning går till!

Vi inför ett särskilt namn på uttrycket innanför absolutbeloppet.

Definition 1
En kvadratisk matris av ordningen 2 (eller en 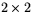-matris) är ett schema med 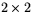tal

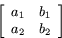
Determinanten av denna matris betecknas 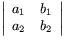och definieras av

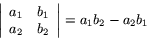
Sats 2
Arean av en parallellogram i 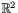som bestäms av vektorerna (a1,b1) och (a2,b2) är absolutbeloppet av determinanten

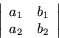
Exempel B
Exempel C  
 
 Sats 3
Följande räkneregler gäller för determinanter av ordningen 2:

(a) Om två rader i en determinant är lika så är determinanten noll. Alltså:

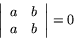
(b) Om två rader byter plats ändrar determinanten tecken:

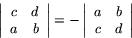
(c) Determinantens värde ändrar inte värde om man till en rad adderar en annan rad multiplicerad med ett tal. Exempelvis gäller:

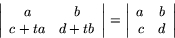
Dessutom gäller

(d)


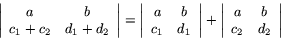
(e)
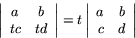
Bevis av sats 3
Geometrisk illustration av räknelag (c)
Exempel D

 
Med hjälp av determinantbegreppet kan definitionen av kryssprodukt omformuleras på följande sätt.

Sats 4
Om 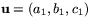och 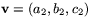så ges kryssprodukten 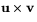av formeln

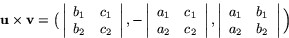
Detta är en direkt följd av defintion 2 i sektion 3.2.

Sats 5
Låt 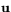och 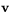vara två vektorer i rummet 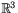. Arean av en parallellogram som bestäms av 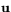och 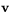är längden av kryssprodukten 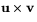, alltså


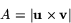
Bevis av sats 5

Exempel E

 


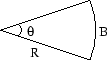
En cirkel har radien 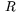. Drag två linjestycken från cirkelns medelpunkt ut till periferin. Därmed har vi delat cirkelskivan i två delar. Vi kallar dessa delar för cirkelsektorer. (Figuren visar en av dessa delar!)

Om 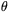är en av de två vinklarna mellan linjestyckena så kommer cirkelsektorns båge 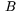att uppta 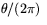av hela cirkelns omkrets, som ju är 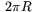. Längden av bågen är alltså


Arean 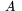av cirkelsektorn kan beräknas på liknande sätt. Arean är ju 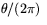av hela cirkeln area, som är 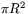. Alltså är

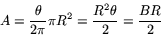
Exempel F


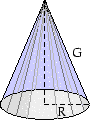
En rät cirkulär kon har en bas som utgörs av en cirkel och konens topp ligger rakt ovanför bascirkelns medelpunkt.
Antag att den cirkulära basen har radien 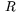och att avståndet från toppen till en punkt på bascirkelns periferi är 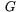. Vi kan då beräkna konens area genom att klippa ut konen längs en linje från toppen till en punkt på bascirkeln och breda ut konytan till ett plan.
Visa hur det går till!