Bevis av sats 1
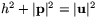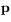Med beteckningar enligt figuren ger Pythagoras sats att , där är den ortogonala projektionen av 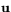längs 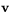. Alltså är

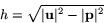
Därför ger formeln (1) att

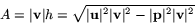
Nu observerar vi att

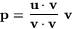
Detta ger

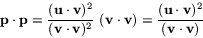
Alltså har vi att

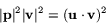
vilket insatt i formeln ovan ger satsens uttryck för arean.

Exempel A
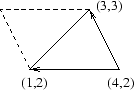
En triangel i planet har hörn i punkterna 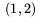, 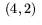och 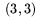. Vi söker triangelns area.


Arean av triangeln är hälften av arean av den parallellogram som bestäms av vektorerna

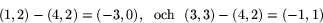
Enligt sats 1 är arean av denna parallellogram

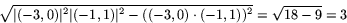
Arean av triangeln är alltså 3/2. Vi utgår från formeln

A2 =( a12+b12 ) ( a22+b22 ) - ( a1a2+b1b2 )2

I denna formel är det högra ledets första produkt lika med

a12 a22 +a12 b22 +b12 a22 +b12 b22

Den andra termen i det högra ledet är

a12a22+b12b22+2a1a2b1b2

Skillnaden mellan dessa två uttryck är A2, alltså:

A2 = a12 b22 +a22b12 -2a1b2a2b1 = (a1b2-a2b1)2

Arean av den parallellogram som bestäms av 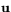och 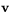blir alltså

A=| a1b2-a2b1 |

Exempel B
Använd determinanter för att beräkna arean av den triangel som har hörn i A, B, C i följande två fall:

(a)
A=(0,0), B=(3,1), C=(2,-3)

Arean är=

 
(b)
A=(2,-4), B=(3,1), C=(-3,-2)

Arean är=

 
 

Exempel C


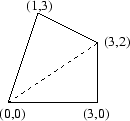
Arean av en fyrhörning som inte är en parallellogram kan lätt beräknas genom att man delar upp fyrhörningen i trianglar. (Samma knep kan användas för femhörningar, sexhörningar osv.) Vi illustrerar med ett exempel. Antag att fyrhörningen har hörn i punkterna 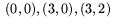och .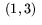
Arean av triangeln med hörn i de tre första punkterna är

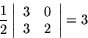
Arean av den andra triangeln är

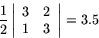
Fyrhöningens area är alltså 6.5.

Testövning
Använd determinater för att beräkna arean av den fyrhörning som har hörn i punkterna (1,2), (3,4), (5, 3), (4,0)!

Arean är=
 

Bevis av sats 3
Räknelagarna (a) och (b) följer direkt ur definitionen, medan (c) följer ur (a), (d) och (e), eftersom

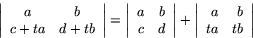
Höger led är lika med

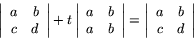
Vi nöjer oss med att visa (d). Enligt definitionen av determinanten är

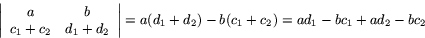
Höger led överensstämmer nu med höger led i formeln (d). Formeln (e) visas analogt.

 

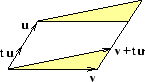
Räknelagarna i satsen kan ges en geometrisk tolkning. Exempelvis innebär räknelagen (c) att den parallellogram som bestäms av vektorerna 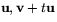har samma area som den som bestäms av 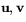. Figuren illustrerar detta!
Exempel D
Man vet att

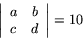
Vad är då värdet av de båda determinanterna

=  
=  
 

 
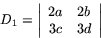
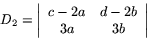
 Bevis av sats 5
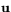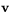Arean av parallellogrammen som bestäms av och är

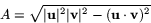
Vi beräknar nu uttrycket under rottecknet i höger led. Först observerar vi att

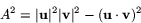
Skriver vi ut det högra ledet får vi att

A2=(a12+b12+c12)(a22+b22+c22)
-(a1 a2+b1 b2+c1 c2)2

Vi utvecklar kvadraterna i höger led och multiplicera ihop. Vissa termer, som till exempel a12 a22, tar då ut varandra och höger led blir

a12 b22+a12c22+b12a22+b12ac22+c12a22+c12b22
-2a1a2b1b2-2a1a2c1c2-2b1b2c1c2

Detta är en summa av tre kvadrater, nämligen

A2 = (b1c2-b2c1)2+(a1c2-a2c1)2 +(a1b2-a2b1)2

Men höger led är inget annat än 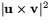. Detta visar satsen.
Exempel E
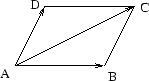
Låt oss beräkna arean av den parallellogram vars hörn är

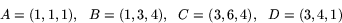
Först kommenterar vi den naturliga frågan: Hur vet man att punkterna bildar hörn i en parallellogram? Svaret är enkelt. Bilda de tre vektorerna

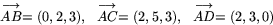
Att ABCD är en parallellogram följer nu av att




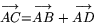
Arean är nu längden av kryssprodukten

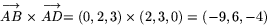
Arean är alltså .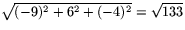

Testövning
Använd kryssprodukten för att beräkna arean av den rymdtriangel som har hörn i punkterna (1,2,3), (-1,3,3), (3,2,4)

Arean är=  
 

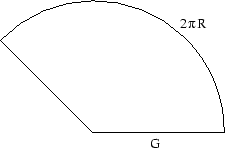
Klipper ut konen längs en linje från toppen till en punkt på bascirkeln och bred ut konens yta. Man får då en cirkelsektor vars radie är 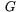och vars båge är 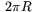(omkretsen av bascirkeln).


Konens area är alltså

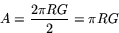
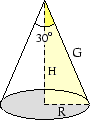
Exempel G


En rät cirkulär kon har öppningsvinkeln 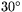och höjden H=10. Beräkna konens area!
Lösning
 Den cirkulära basen har radien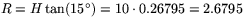
Med Pythagoras sats får man 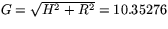. Alltså är arean .

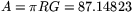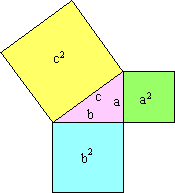
I den grekiska matematiken var Pythagoras sats en relation mellan tre kvadraters areor!