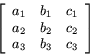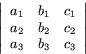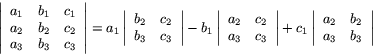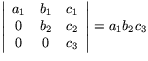Parallellepipeder är tredimensionella motsvarigheter till parallellogrammer. En parallellepiped begränsas av sex plan som är parvis parallella, så som figuren försöker illustrera.

Sats 1
Volymen av en parallellepiped som bestäms av vektorerna , och är absolutbeloppet av

Om , och så är

Bevis av sats 1

Exempel A
En parallellepiped har ett hörn i origo och bestäms av vektorerna

Vi skall bestämma koordinaterna för parallellepipedens åtta hörn och dess volym.
Visa en lösning
 
Definition 1
En kvadratisk matris av ordningen 3 (eller en -matris) är ett schema med tal

Determinanten av denna matris betecknas

och definieras av

Absolubeloppet av determinanten är volymen av en parallellepiped som bestäms av vektorerna i determinantens tre rader. Se sats 1.
Sats 2(Några räkneregler för determinanter)
(a) Om två rader i en determinant är lika så är determinanten noll.
(b) Om två rader byter plats ändrar determinanten tecken.
(c) Determinantens värde ändras inte om man till en rad adderar en annan rad multiplicerad med ett tal.
(d)
Bevis av sats 2
Exempel B  
 
  

Volymberäkningar
Exempel C
Exempel D

Avgör om tre givna vektorer ligger i ett plan
Med hjälp av determinater kan man avgöra om tre vektorer ligger i samma plan. Om så måste ligga i det plan genom origo vars normal är (om vi nu antar att och inte är parallella). Det omvända gäller ju också!
Exempel E

Ekvationen för ett plan i determinantform
Exempel F