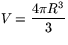Volymen av en parallellepiped är (definerad som) volymen av basytan gånger höjden. Samma idé används för att bestämma volymen av en cylinder. När vi talar om cylindrar tänker vi i första hand på cylindrar med en cirkulär bas.
Om basen är en cirkel med radien R och höjden är H så är arean av bascirkeln 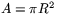 . Volymen av cylindern är
. Volymen av cylindern är
Man kan lika gärna tänka sig att man har ett annat område
som bas.
Läs om detta
 Exempel A
Exempel A
Den mängd vätska som ryms i ett rör kan lätt beräknas med hjälp av formeln för cylinderns volym. Som exempel tar vi ett rör vars innerdiameter är 3 dm och vars längd är 2 meter. Volymen är
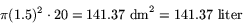
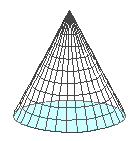
En rät cirkulär kon har en cirkel som bas och konens topp ligger rakt ovanför bascirkelns centrum.
Bascirkelns area är 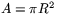 om dess radie antas vara R. Om konens höjd
är H så är konens volym
Volymen av en rät cirkulär kon är alltså en tredjedel av basarean
gånger höjden.
om dess radie antas vara R. Om konens höjd
är H så är konens volym
Volymen av en rät cirkulär kon är alltså en tredjedel av basarean
gånger höjden.
Förklara varför!
Kommentar
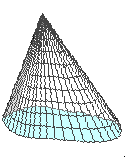
Samma argument kan utan förändring användas för en kon med en annan bas.
Även i detta fall är alltså volymen en tredjedel av basarean
multiplicerat med höjden.
Exempel B
Vi skall här beräkna volymen av en sfär med radien R. Låt oss anta att sfärens medelpunkt ligger i origo. Sfären består då av alla (x,y,z) sådana att
x2+y2+z2 = R2
Volymen av en sfär är
Bevisa denna formel
Om vi vill beräkna arean av en tunn skiva av en sfär kan vi inte ersätta den med ett smal cylinderskiva, eftersom felet då kommer att blir relativt stort.
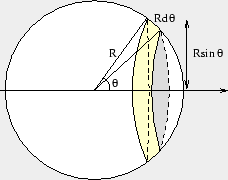
Vi ersätter i stället bandet med en cylinder vars höjd är bågen 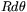 i nästa figur.
i nästa figur.
Det smala bandet i figuren har då bredden 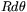 . Eftersom radien av bandet är
. Eftersom radien av bandet är 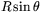 är bandets area ungefär lika med
är bandets area ungefär lika med 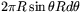 . Hela arean är därför
. Hela arean är därför
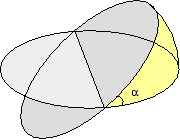
Vi börjar med att studera områden av den typ som figuren beskriver. Områden av detta utseende kallar vi halvmånar.
Observera först att arean av hela sfären är 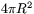 om radien är R. Arean av ett halvklot är därför
om radien är R. Arean av ett halvklot är därför 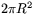 . Därför är arean av området i figuren
. Därför är arean av området i figuren 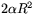 , eftersom området utgör
, eftersom området utgör 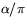 av hela övre halvklotet.
av hela övre halvklotet.
Med hjälp av denna observation kan man visa följande sats.
Sats 1
Vinkelsumman i en sfärisk triangel är alltid större än 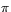 (
(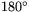 ). Arean av en sfärisk triangel är kvadraten på sfärens radie multiplicerad med skillnaden mellan vinkelsumman och
). Arean av en sfärisk triangel är kvadraten på sfärens radie multiplicerad med skillnaden mellan vinkelsumman och 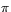 .
.
Bevis
På senare år har förutsättningarna för navigation på världshaven
förändrats radikalt. Redan tillkomsten av radiofyrar underlättade
navigationen. Med hjälp av ett system av satelliter har navigationen
ytterligare förenklats. Att bestämma sin position har varit möjligt
långt tidigare, men problemet att finna sin position utan moderna
hjälpmedel är inte alls enkelt. Vi skall här beskriva hur man kan
göra. Först beskriver vi hur man finner sin latitud-det är inte så
svårt. Sedan beskriver vi hur man i princip kan finna sin longitud-ett
svårare problem.
Latitudproblemet - sextanten
Longitudproblemet - sextanten och kronometern
Satelitnavigation - GPS
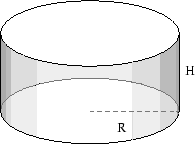
![]() . Volymen av cylindern är
. Volymen av cylindern är
![]() Exempel A
Exempel A![]()