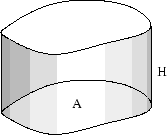
Låt alltså 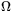 vara ett område i xy-planet. Cylindern med
vara ett område i xy-planet. Cylindern med 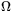 som bas består då av alla punkter (x,y,z) i rummet sådana att
som bas består då av alla punkter (x,y,z) i rummet sådana att 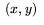 ligger i området
ligger i området 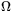 och
och 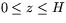 , där H är cylinderns höjd. Om man känner arean A av
, där H är cylinderns höjd. Om man känner arean A av 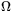 så får man cylinderns volym med formeln.
så får man cylinderns volym med formeln.
V= AH
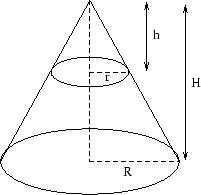
Om vi skär av en bit av konen med ett snitt som är parallellt med bascirkelns plan så kommer snittet att vara en cirkel vars radie bestäms av på vilken höjd snittet görs. Antag att snittet läggs på avståndet h från toppen.
I figuren kan vi betrakta konen i toppen som en förminskad version av hela konen. Förminskningen av sträckor har skett i skalan
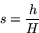
Den lilla toppkonens bascirkel har därför radien r = s R. Dess area är alltså 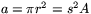 . Arean förminskas alltså som kvadraten på längdskalan dvs i skalan s2. Vi tänker oss nu att vi skär ut en tunn skiva med höjden dh ur konen. Dess volym är då ungefär så stor som volymen av en cylinder med höjden dh och basarea a. Volymen av denna cylinder är
. Arean förminskas alltså som kvadraten på längdskalan dvs i skalan s2. Vi tänker oss nu att vi skär ut en tunn skiva med höjden dh ur konen. Dess volym är då ungefär så stor som volymen av en cylinder med höjden dh och basarea a. Volymen av denna cylinder är
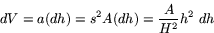 Detta ger
Detta ger
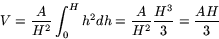
Exempel B
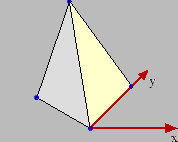
En pyramid har hörn i punkterna

Vi söker dess volym.
Basen är en triangel i xy-planet med hörn i de tre första punkterna. Bastriangelns area är
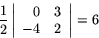
Toppens höjd över xy-plantet är H=5. Volymen är alltså
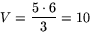
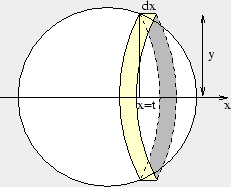
Låt oss skära sfären med ett plan som är parallellt med yz-planet, tex planet x=t. Detta plans snitt med sfären blir då en cirkel med ekvationen y2+z2 = R2-t2, dvs en cirkel med radien 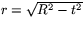 .
.
Vi ser motsvarande cirkelskiva som bas för en cylinder med höjden dt. Dess volym är
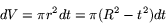
Sfärens volym är därför
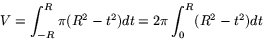
vilket ger
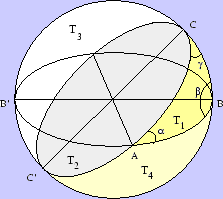
I följande figur har vi ritat en sfärisk triangel ABC. Det plan som skär ut storcirkeln genom B och C har placerats i papperets plan och punkten A ligger ovanför detta plan. Figuren beskriver och ger namn åt fyra områden T1,T2,T3,T4 vilka alla ligger på den halvsfär som ligger över papperets plan. Punkterna B' och C' är antipoderna till B resp. C, dvs de är spegelbilderna i origo av B resp. C. De ligger därför båda i papperets plan. De fyra områden begränsas av sfäriska trianglar.

Låt oss spegla T2 i origo. Vi får då ett område som tillsammans med T1 utgör en halvmåne med vinkeln 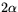 . Spegling lämnar arean oförändrad. Därför måste följande gälla för areorna av figurens sfäriska trianglar
. Spegling lämnar arean oförändrad. Därför måste följande gälla för areorna av figurens sfäriska trianglar
 Av liknade skäl måste
Av liknade skäl måste


Eftersom de fyra områden tillsamman utgör halvklotet över papperets plan är deras sammanlagda area 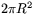 . Summerar vi vänsterleden i de tre ekvationerna ovan får vi därför att
. Summerar vi vänsterleden i de tre ekvationerna ovan får vi därför att
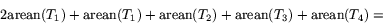
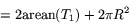 Genom att jämföra med summan av högerleden ser vi att
Genom att jämföra med summan av högerleden ser vi att
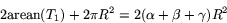 vilket ger
vilket ger
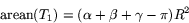
Detta bevisar satsen!
Latitudproblemet - sextanten
Med hjälp av en sextant kan man mäta vinkeln mellan horisont och en himlakropp, låt oss säga en stjärna S.
Om observatören befinner sig i punkten Q på jordytan kan han med hjälp av sextanten mäta vinkeln mellan horisontlinjen och linjen genom Q och stjärnan S. Det är vinkeln 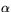 i figuren. Därmed kan han också bestämma vinkeln
i figuren. Därmed kan han också bestämma vinkeln 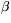 mellan lodlinjen genom Q och jordens medelpunkt O. Det är den linje som i figuren pekar i riktning mot Z, observatörens zenit. Man har ju att
mellan lodlinjen genom Q och jordens medelpunkt O. Det är den linje som i figuren pekar i riktning mot Z, observatörens zenit. Man har ju att
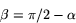
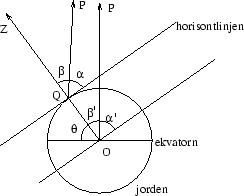
Om man mäter vinkeln mellan horisontlinjen och polstjärnan kan man finna (ett närmevärde till) sin latitud (breddgrad). Latituden är vinkel 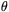 i nästa figur.
i nästa figur.
Polstjärnan befinner sig nämligen tämligen exakt rakt i norr (P i figuren). Man kan då mäta vinkeln 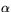 mellan horisontlinjen och polstjärnan. Eftersom polstjärnan befinner sig långt bort kommer de båda linjerna QP och OP att vara praktiskt taget parallella. Det innebär att vinkeln
mellan horisontlinjen och polstjärnan. Eftersom polstjärnan befinner sig långt bort kommer de båda linjerna QP och OP att vara praktiskt taget parallella. Det innebär att vinkeln 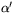 och
och 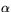 är ungefär lika. Eftersom
är ungefär lika. Eftersom 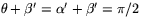 så är
så är 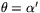 . Det följer att
. Det följer att 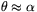 .
.
Därmed har vi fått ett närmevärde på observatörens latitud. Vi har också indirekt mätt vinkeln mellan observatörens zenit och polstjärnan, dvs vinkeln 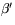 i figuren (
i figuren (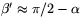 ).
).
Longitudproblemet - sextanten och kronometern
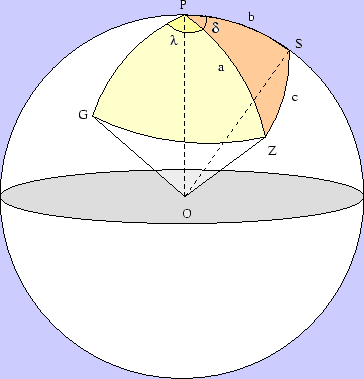
Longitudproblemet är problemet att finna sin longitud. För att lösa detta behöver man mäta mot två stjärnor, låt oss säga polstjärnan P och ytterligare en stjärna S. Vi tänker oss en stor sfär med centrum i jordens medelpunkt. På sfären avsätter vi punkter som får representera stjärnorna och observatörens zenit. Vi drar alltså linjer genom jordens medelpunkt och de olika stjärnorna och genom observatörens zenit. Vi drar också en linje genom jordens medelpunt och Greenwich. Det är punkten G i figuren nedan. Den stora sfären kallar vi himmelssfären. Med hjälp av sextant kan observatören bestämma vinklarna mellan zenit och polstjärnan och mellan zenit och stjärnan S. Man kan alltså mäta storcirkelbågarna a och c i nästa figur.
Observera att även storcirkelbågen 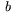 är känd, ty det är bågen mellan två kända stjärnor. Man kan alltså ha med sig en tabell i vilken
är känd, ty det är bågen mellan två kända stjärnor. Man kan alltså ha med sig en tabell i vilken 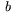 kan avläsas. Sidorna i den astronomiska grundtriangeln
kan avläsas. Sidorna i den astronomiska grundtriangeln 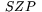 är därmed kända. Med hjälp av cosinussatsen för sfäriska trianglar kan man då beräkna vinkeln
är därmed kända. Med hjälp av cosinussatsen för sfäriska trianglar kan man då beräkna vinkeln  .
.
Med detta är inte mycket vunnet, ty jorden roterar kring sin axel. Vinkeln  varierar alltså med tiden på dygnet, liksom vinkeln mellan
varierar alltså med tiden på dygnet, liksom vinkeln mellan 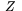 och
och 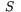 . Men antag nu att man har en kronometer med vars hjälp man kan avläsa vad en klocka i Greenwhich visar det ögonblick på dygnet då observationen gjordes. Antag vidare att man har med sig en tabell i vilken man har noterat motsvarande mätningar mot stjärnan
. Men antag nu att man har en kronometer med vars hjälp man kan avläsa vad en klocka i Greenwhich visar det ögonblick på dygnet då observationen gjordes. Antag vidare att man har med sig en tabell i vilken man har noterat motsvarande mätningar mot stjärnan 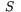 utförda i Greenwhich vid olika tider på dygnet. Man kan då tillämpa cosinussatsen på grundtriangeln
utförda i Greenwhich vid olika tider på dygnet. Man kan då tillämpa cosinussatsen på grundtriangeln 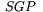 och beräkna vinkeln
och beräkna vinkeln  , dvs vinkeln
, dvs vinkeln 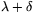 . Genom att subtrahera den nyss beräknade vinkeln
. Genom att subtrahera den nyss beräknade vinkeln  kan man bestämma vinkeln
kan man bestämma vinkeln 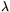 . Men detta är just observatörens longitud-longitudproblemet är löst!
. Men detta är just observatörens longitud-longitudproblemet är löst!
Sextanten räcker tydligen inte för att bestämma sin longitud. Man
behöver en säker kronometer och man behöver tabeller över mätningar
som gjorts mot vissa standardstjärnor vid olika tidpunkter på dygnet
från en plats vars longitud är känd-här valde vi Greenwich.
Satellitnavigation - GPS
Det finns i dag ett system (GPS-systemet, General Postitioning System) med satelliter som kontinuerligt sänder ut information om sin position. Genom att avläsa den tid det tar för satellitsignalen att nå observatören kan han bestämma på vilket avstånd från satelliten han befinner sig. Därmed får han veta att han befinner sig på en sfär med en viss radie och en viss känd medelpunkt. Genom att ta emot signaler från flera satelliter får han veta att han samtidigt befinner sig på andra sfärer. I princip räcker det att ta emot signaler från tre satelliter. Observatören kan då bestämma sin position som är en punkt som är gemensam mellan tre sfärer med kända radier och medelpunkter. I praktiken kan fler satelliter behövas för att uppnå en tillräcklig nogrannhet.
Bilden föreställer en sfärisk triangel

![]()
![]()
![]()
![]()
![]()

![]() . Spegling lämnar arean oförändrad. Därför måste följande gälla för areorna av figurens sfäriska trianglar
. Spegling lämnar arean oförändrad. Därför måste följande gälla för areorna av figurens sfäriska trianglar 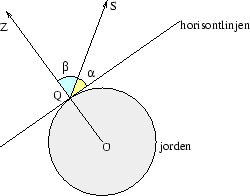
![]() i figuren. Därmed kan han också bestämma vinkeln
i figuren. Därmed kan han också bestämma vinkeln ![]() mellan lodlinjen genom Q och jordens medelpunkt O. Det är den linje som i figuren pekar i riktning mot Z, observatörens zenit. Man har ju att
mellan lodlinjen genom Q och jordens medelpunkt O. Det är den linje som i figuren pekar i riktning mot Z, observatörens zenit. Man har ju att
![]()
![]() i nästa figur.
i nästa figur.
![]() mellan horisontlinjen och polstjärnan. Eftersom polstjärnan befinner sig långt bort kommer de båda linjerna QP och OP att vara praktiskt taget parallella. Det innebär att vinkeln
mellan horisontlinjen och polstjärnan. Eftersom polstjärnan befinner sig långt bort kommer de båda linjerna QP och OP att vara praktiskt taget parallella. Det innebär att vinkeln ![]() och
och ![]() är ungefär lika. Eftersom
är ungefär lika. Eftersom ![]() så är
så är ![]() . Det följer att
. Det följer att ![]() .
.![]() i figuren (
i figuren (![]() ).
).
![]() är känd, ty det är bågen mellan två kända stjärnor. Man kan alltså ha med sig en tabell i vilken
är känd, ty det är bågen mellan två kända stjärnor. Man kan alltså ha med sig en tabell i vilken ![]() kan avläsas. Sidorna i den astronomiska grundtriangeln
kan avläsas. Sidorna i den astronomiska grundtriangeln ![]() är därmed kända. Med hjälp av cosinussatsen för sfäriska trianglar kan man då beräkna vinkeln
är därmed kända. Med hjälp av cosinussatsen för sfäriska trianglar kan man då beräkna vinkeln ![]() .
.![]() varierar alltså med tiden på dygnet, liksom vinkeln mellan
varierar alltså med tiden på dygnet, liksom vinkeln mellan ![]() och
och ![]() . Men antag nu att man har en kronometer med vars hjälp man kan avläsa vad en klocka i Greenwhich visar det ögonblick på dygnet då observationen gjordes. Antag vidare att man har med sig en tabell i vilken man har noterat motsvarande mätningar mot stjärnan
. Men antag nu att man har en kronometer med vars hjälp man kan avläsa vad en klocka i Greenwhich visar det ögonblick på dygnet då observationen gjordes. Antag vidare att man har med sig en tabell i vilken man har noterat motsvarande mätningar mot stjärnan ![]() utförda i Greenwhich vid olika tider på dygnet. Man kan då tillämpa cosinussatsen på grundtriangeln
utförda i Greenwhich vid olika tider på dygnet. Man kan då tillämpa cosinussatsen på grundtriangeln ![]() och beräkna vinkeln
och beräkna vinkeln ![]() , dvs vinkeln
, dvs vinkeln ![]() . Genom att subtrahera den nyss beräknade vinkeln
. Genom att subtrahera den nyss beräknade vinkeln ![]() kan man bestämma vinkeln
kan man bestämma vinkeln ![]() . Men detta är just observatörens longitud-longitudproblemet är löst!
. Men detta är just observatörens longitud-longitudproblemet är löst!
