Exempel A
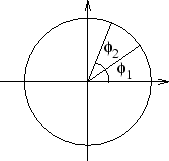
Om vi sätter samman en rotation kring origo med en annan rotation
kring origo får man en ny rotation kring origo. Mer precist,
sammansättningen av rotation med vinkeln 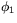 med rotation
vinkeln
med rotation
vinkeln 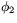 ger rotation vinkeln
ger rotation vinkeln 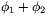 . Med de
tidigare använda beteckningarna för rotation har vi alltså att
. Med de
tidigare använda beteckningarna för rotation har vi alltså att
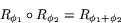
Denna formel utsäger något ganska självklart: Om man först roterar
en viss vinkel runt origo och sedan roterar en annan vinkel blir den
sammantagna effekten densamma som att rotera med de två vinklarnas
summa!
Om man vill räkna ut hur 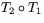 påverkar planets vektorer så tar
vi en vektor
påverkar planets vektorer så tar
vi en vektor 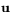 och beräknar
och beräknar 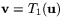 . Sedan använder vi
transformationen T2 på
. Sedan använder vi
transformationen T2 på 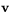 och bildar
och bildar 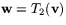 . Den
sammansatta avbildningen
. Den
sammansatta avbildningen 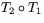 är då avbildningen
är då avbildningen 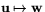 . Detta innebär att
. Detta innebär att 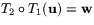 . Eftersom
. Eftersom
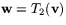 och
och 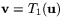 innebär detta att
innebär detta att
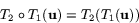
Observera att ordningen är väsentlig. I regel är avbildningarna 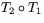 och
och 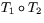 inte lika!
Talen i matrisen
inte lika!
Talen i matrisen 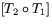 består av
skalärprodukter mellan raderna i [T2] och kolonnerna
(kolumnerna) i [T1]. De två raderna i [T2] definierar ju två
vektorer, nämligen (a11,a12) och (a21,a22). De två
kolonnerna i [T1] definierar också två vektorer,
nämligen (b11,b21) och (b12,b22). Talen som står i
matrisen för
består av
skalärprodukter mellan raderna i [T2] och kolonnerna
(kolumnerna) i [T1]. De två raderna i [T2] definierar ju två
vektorer, nämligen (a11,a12) och (a21,a22). De två
kolonnerna i [T1] definierar också två vektorer,
nämligen (b11,b21) och (b12,b22). Talen som står i
matrisen för 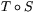 är nu de fyra skalärprodukter som kan
bildas mellan dessa två par av vektorer:
är nu de fyra skalärprodukter som kan
bildas mellan dessa två par av vektorer:
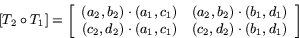
Bevis (av sats 1)
Sätt 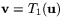 och
och 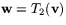 . Då är
. Då är 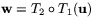 . Beviset går ut på att helt rått räkna ut hur
koordinaterna för
. Beviset går ut på att helt rått räkna ut hur
koordinaterna för 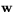 ser ut uttryckt i koordinaterna för
ser ut uttryckt i koordinaterna för
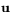 . Eftersom
. Eftersom 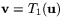 har vi att
har vi att
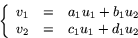
Sambandet 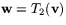 ger på samma sätt
ger på samma sätt
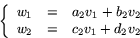
Sätter vi in formlerna för 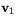 och
och 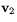 så får vi
så får vi
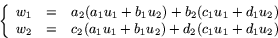
Samlar man nu ihop koefficienterna framför u1 och u2 i
höger led får man
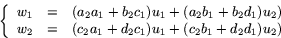
Detta beskriver den sammansatta avbildningen 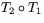 och bevisar
satsens formel.
och bevisar
satsens formel.
Exempel B
Vi undersöker sammansättningen av två skevavbildningar med
matriserna
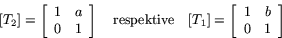
Matrisen för sammansättningen är
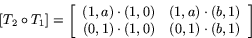
Detta ger
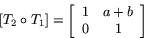
Sammansättning av två skevavbildningar är alltså en ny
skevavbildning.
Exempel C
Låt oss beräkna sammansättningen av spegling i x-axeln , alltså S0, med spegling i y-axeln, alltså 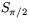 . Dessa har matriserna
. Dessa har matriserna
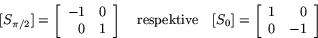
Vi betraktar den sammansatta avbildningen 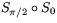 alltså först spegling i x-axeln sedan spegling i y-axeln. Den har matrisen
alltså först spegling i x-axeln sedan spegling i y-axeln. Den har matrisen
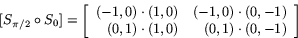
det vill säga
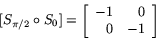
Detta visar att den sammansatta avbildningen 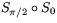 är avbildningen
är avbildningen 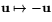 , vilket är spegling i origo eller (ekvivalent) rotation med vinkeln
, vilket är spegling i origo eller (ekvivalent) rotation med vinkeln 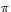 .
.
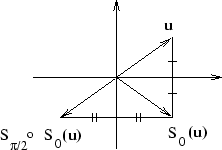
Figuren visar varför 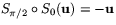 .
.
Exempel D
Talen i produkten M2 M1 består alltså av skalärprodukter mellan
raderna i matrisen M2 och kolonnerna i matrisen M1, alltså
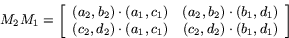 Testövning
Testövning
Sätt
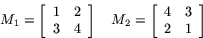 Då är
Då är
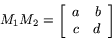 Mata in rätt värden:
Mata in rätt värden:
Alldeles rätt !
Observera att ordningen mellan faktorerna i produkten
M2 M1 är väsentlig. I regel är
produkterna M2 M1 och
M1 M2 inte lika.
Här får man:
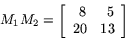
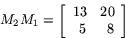 Fel svar, kolla din beräkningar igen!
Fel svar, kolla din beräkningar igen!
Observera att ordningen mellan faktorerna i produkten
M2 M1 är väsentlig. I regel är
produkterna M2 M1 och
M1 M2 inte lika.
Det är fel på någon formel du har matat in!
Exempel E
Vi studerar sammansättning mellan (olikformig) skalförändring och rotation
kring origo. Låt oss säga att vi fördubblar skalan i den lodräta
axelns riktning men lämnar skalan oförändrad i den vågräta
axelns riktning. Det finns två fall. Antingen gör man
skaländringen först och roterar sedan eller också roterar man
först och gör skaländringen därefter. Man inser att resultatet
inte kommer att bli lika i dessa två fall.
Figuren visar effekten av de båda avbildningarna med vinkeln 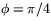 .
.
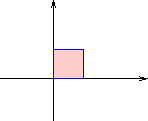
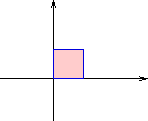
I den vänstra figuren visas vad händer med den markerade kvadraten om
man först roterar 45 grader runt origo och
sedan fördubblar skalan längs den lodräta axeln.
I den högra figuren visas vad händer med den markerade kvadraten om
man först förlänger skalan längs den lodräta axeln och
sedan roterar 45 grader runt origo.
Man kan också undersöka de båda sammansättningarna genom att beräkna matriserna för de sammansatta
avbildningarna.
Visa hur detta går till!
Den transformation som fördubblar skalan i den lodräta
axelns riktning men lämnar skalan oförändrad i den vågräta
axelns riktning har matrisen
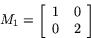 Rotation kring origo med vinkeln
Rotation kring origo med vinkeln 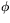 har matrisen
har matrisen
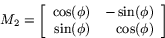 Den sammansatta avbildning man får genom att först göra
skaländringen och sedan rotera har matrisen
Den sammansatta avbildning man får genom att först göra
skaländringen och sedan rotera har matrisen
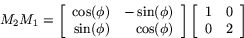
Detta ger
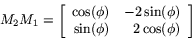
På liknande sätt kan man ta fram matrisen för den sammansatta avbildning man får genom att först rotera och sedan
göra skaländringen!
Visa detta!
Den sammansatta avbildning man får genom att först rotera och sedan
göra skaländringen har matrisen
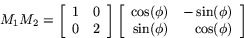 vilket ger
vilket ger
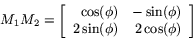
Man ser att
Exempel F
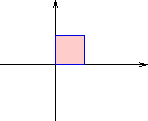
I den vänstra figuren visas vad händer med den markerade kvadraten om
man först roterar 45 grader runt origo och
sedan speglar i den vågräta axeln.
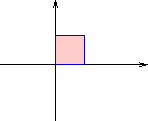
I den högra figuren visas vad händer med den markerade kvadraten om
man först speglar i den vågräta axeln och
sedan roterar 45 grader runt origo.
Vi undersöker hur matriserna ser ut i de båda fallen.
Visa!
Låt S0 vara spegling i den vågräta axeln. Vi vet då att matrisen för S0 är
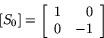 Låt oss nu sätta samman S0 med rotationen
Låt oss nu sätta samman S0 med rotationen 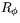 . Återigen finns det två sätt att bilda sammansättningar. Antingen bildar vi
. Återigen finns det två sätt att bilda sammansättningar. Antingen bildar vi 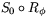 eller också tar vi avbildningar i den omvända ordningen och bildar
eller också tar vi avbildningar i den omvända ordningen och bildar 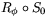 .Enligt sats 1 är matrisen för
.Enligt sats 1 är matrisen för 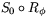 lika med
lika med
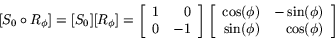 Räknar man ut matrisprodukten i det högra ledet så får man
Räknar man ut matrisprodukten i det högra ledet så får man
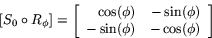
På liknande sätt kan vi beräkna matrisen för 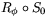 genom att bilda produkten
genom att bilda produkten 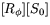 .
Visa resultatet!
.
Visa resultatet!
Man får att
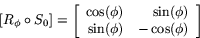
Man ser att matriserna för 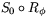 och
och 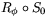 är olika (om
är olika (om 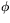 inte är ett heltal multiplicerat med
inte är ett heltal multiplicerat med 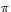 ). Eftersom matrisavbildningar bestäms av sina matriser så visar detta att
). Eftersom matrisavbildningar bestäms av sina matriser så visar detta att
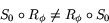
Exempel G
Vi studerar sammansättning av spegling i linjen y=x följd av spegling i y-axeln.
Spegling i linjen y=x är transformationen 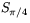 medan spegling i y-axeln är transformationen
medan spegling i y-axeln är transformationen 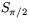 . Den sammansatta avbildningen
. Den sammansatta avbildningen 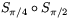 har då matrisen
har då matrisen
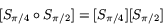 Nu är
Nu är
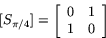
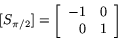 Därför är
Därför är
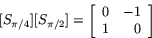
Höger led är matrisen för rotation vinkeln 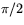 , alltså
, alltså
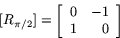
Eftersom således 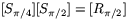 drar vi slutsatsen att
drar vi slutsatsen att
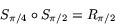

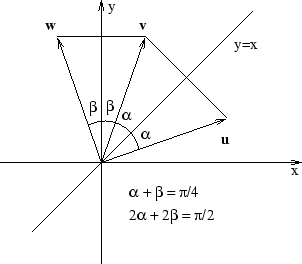
I figuren är 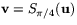 och
och 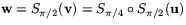 , samtidigt som
, samtidigt som 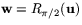 .
.
Exempel H
Vi skall här undersöka vad som händer om man sätter samman två speglingar 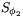 och
och 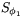 . Lite överaskande skall vi se att
sammansättningen blir en rotation. Man kan övertyga sig om
det med hjälp av ett geometriskt argument, men vi skall här först använda matrismultiplikation för att komma fram till resultatet.
. Lite överaskande skall vi se att
sammansättningen blir en rotation. Man kan övertyga sig om
det med hjälp av ett geometriskt argument, men vi skall här först använda matrismultiplikation för att komma fram till resultatet.
Först konstaterar vi att
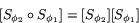 Höger led är matrisprodukten
Höger led är matrisprodukten
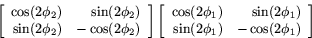 Med hjälp av subtraktionsformlerna för sinus och cosinus får man att denna produkt är
Med hjälp av subtraktionsformlerna för sinus och cosinus får man att denna produkt är
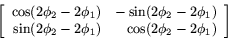
Denna matris känner vi igen som matrisen för rotation med vinkeln 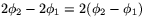 . Alltså har vi att
. Alltså har vi att
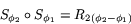

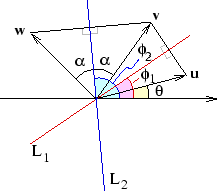
I figuren är 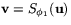 ,
, 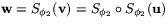 . Vinkeln mellan
. Vinkeln mellan 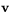 och linjen L1 i figuren är
och linjen L1 i figuren är 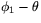 . Därför är vinkeln mellan
. Därför är vinkeln mellan 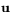 och
och 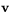 lika med
lika med 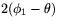 . Om då
. Om då 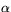 är vinkeln mellan
är vinkeln mellan 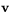 och linjen L2 i figuren så har vi att
och linjen L2 i figuren så har vi att 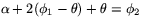 . Detta ger
. Detta ger 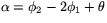 . Vinkeln mellan
. Vinkeln mellan 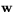 och
och 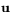 är alltså
är alltså
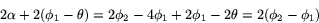
Detta visar på nytt att
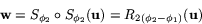
![]() med rotation
vinkeln
med rotation
vinkeln ![]() ger rotation vinkeln
ger rotation vinkeln ![]() . Med de
tidigare använda beteckningarna för rotation har vi alltså att
. Med de
tidigare använda beteckningarna för rotation har vi alltså att
![]()