Man kan tolka determinanten av en matrisavbildning som en area.
Sätt nämligen 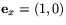 och
och 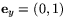 och antag att
T har matrisen M. Då är
och antag att
T har matrisen M. Då är
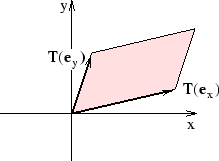
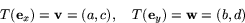 Den parallellogram som bestäms av
Den parallellogram som bestäms av
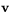 och
och 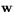 arean |ad-cb|, vilket är absolutbeloppet av
arean |ad-cb|, vilket är absolutbeloppet av
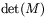 . Det innebär att absolutbeloppet av determinanten för
avbildningen T är arean av den parallellogram som bestäms av
bilderna av basvektorerna
. Det innebär att absolutbeloppet av determinanten för
avbildningen T är arean av den parallellogram som bestäms av
bilderna av basvektorerna 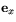 och
och 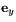 .
.
Anmärkning Två vektorer 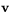 och
och 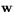 som inte är parallella definierar en parallellogram. I sats 1 kan det emellertid inträffa att
som inte är parallella definierar en parallellogram. I sats 1 kan det emellertid inträffa att 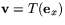 och
och 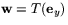 är parallella. Dessa vektorer definerar då egentligen inte en parallellogram i vanlig mening utan en parallellogram som har kolapsat. Man brukar tala om en urartad parallellogram. En sådan ges arean . Med denna konvention är satsen korrekt oavsett om bilderna av
är parallella. Dessa vektorer definerar då egentligen inte en parallellogram i vanlig mening utan en parallellogram som har kolapsat. Man brukar tala om en urartad parallellogram. En sådan ges arean . Med denna konvention är satsen korrekt oavsett om bilderna av 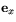 och
och 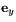 är parallella eller inte.
är parallella eller inte.
Exempel A
Rotation vinkeln 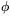 (med origo som rotationscentrum), alltså avbildningen
(med origo som rotationscentrum), alltså avbildningen 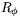 , har matrisen
, har matrisen
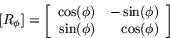
Determinanten är
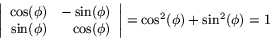
Exempel B
Spegling 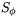 i den linje genom origo som bildar vinkeln
i den linje genom origo som bildar vinkeln 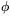 mot högra halvan av x-axeln har determinanten
mot högra halvan av x-axeln har determinanten
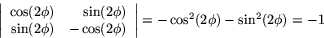
Både spegling och rotation har alltså egenskapen att arean av den parallellogram som bestäms av bilderna av enehtsvektorerna 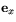 och
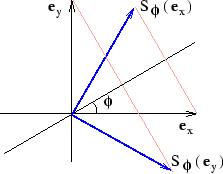
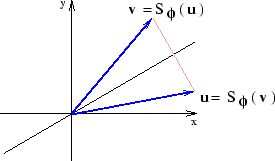
och 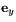 har arean 1. Arean av bilderna är ju absolutbeloppet av determintanen. Minustecknet i kalkylen ovan spelar alltså ingen roll när det gäller arean. Likväl har minustecknet en geometrisk betydelse. Det beror nämligen på att spegling kastar om orienteringen, vilket inte rotation gör. För att förklara detta tänker vi oss att man vrider
har arean 1. Arean av bilderna är ju absolutbeloppet av determintanen. Minustecknet i kalkylen ovan spelar alltså ingen roll när det gäller arean. Likväl har minustecknet en geometrisk betydelse. Det beror nämligen på att spegling kastar om orienteringen, vilket inte rotation gör. För att förklara detta tänker vi oss att man vrider 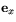 vinkeln
vinkeln 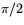 så att den sammanfaller med
så att den sammanfaller med 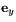 . Man måste då vrida i positiv orientering (moturs). Men om man vill vrida bilden
. Man måste då vrida i positiv orientering (moturs). Men om man vill vrida bilden 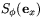 vinkeln
vinkeln 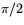 så att den sammanfaller med
så att den sammanfaller med 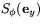 så måste man vrida i negativ orientering (medurs). Figuren illustrerar detta.
så måste man vrida i negativ orientering (medurs). Figuren illustrerar detta.
Exempel C
Ortogonal projektion 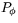 på den linje genom origo som bildar vinkeln
på den linje genom origo som bildar vinkeln
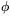 mot högra halvan av x-axeln har matrisen
mot högra halvan av x-axeln har matrisen
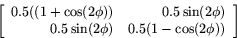
Determinanten är alltså
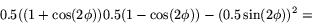
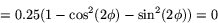
Detta stämmer väl med satsen, ty bilderna av 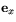 och
och 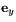 kommer ju att hamna på linjen och är alltså parallella. Arean av den urartade parallellogram som bilderna spänner upp är alltså .
kommer ju att hamna på linjen och är alltså parallella. Arean av den urartade parallellogram som bilderna spänner upp är alltså .
Exempel D
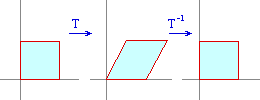
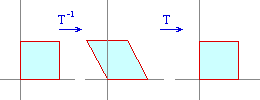
Låt T vara skevavbildningen med matrisen
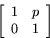
Vad är arean av bilden av rektangeln med hörn i origo och punktenra (2,0), (2,3) och (0,3)?
 ösning
ösning
Bilden av rektangeln är den parallellogram som bestäms av vektorerna
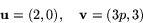
Arean av bilden är alltså 6
oberoende av värdet på p
Vi undersöker inverterbarheten hos tre naturliga exempel, nämligen
rotation,
spegling och
ortogonal projektion
Exempel F
Rotation kring origo med vinkeln 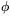 , alltså avbildningen
, alltså avbildningen 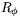 , är inverterbar. Varje vektor
, är inverterbar. Varje vektor 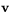 är bild av precis en vektor
är bild av precis en vektor 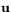 och man kan finna vektorn
och man kan finna vektorn 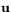 genom att rotera
genom att rotera 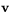 vinkeln
vinkeln 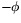 . Man har alltså att om
. Man har alltså att om 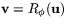 så är
så är 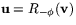 . Rotation med vinkeln
. Rotation med vinkeln 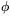 är alltså inverterbar med inversen
är alltså inverterbar med inversen
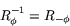
Exempel G
Spegling i en linje (genom origo) är också en inverterbar avbildning av 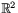 på sig själv. Om nämligen
på sig själv. Om nämligen 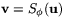 så är
så är 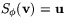 .
Det innebär att
.
Det innebär att
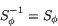
Exempel H
Ortogonal projektion i en linje är inte inverterbar. Om vi antar att linjen är ax+by=0 så kommer varje vektor som är parallell med normalen (a,b) att avbildas på (0,0), så avbildningen är inte injektiv.
Exempel I
Vi vet redan att 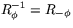 . Låt oss här verifiera denna formel med hjälp av satsen ovan. Matrisen för
. Låt oss här verifiera denna formel med hjälp av satsen ovan. Matrisen för 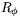 är
är
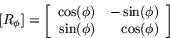
Determinanten av denna matris är 1. Satsen säger då att avbildningen 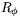 är inverterbar och att inversens matris är
är inverterbar och att inversens matris är
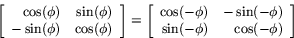
Men detta är inget annat än matrisen för 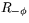 . Alltså är
. Alltså är 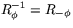 .
.
Exempel J
Antag att T har matrisen
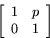
Avbildningen T är alltså en skevavbildning. Matrisens determinant är 1. Satsen visar att T är inverterbar och att inversen är en matrisavbildning med matrisen
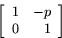
Exempel K
Låt T vara matrisavbildningen med matris
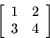
Bestäm matrisen för inversen!
Svar:
Inversen har matrisen
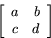 där
där
Bevis(av produktformeln för determinanter)
Låt oss sätta
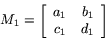 ,
,
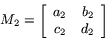 Då är
Då är
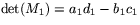 ,
, 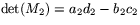 Alltså är
Alltså är
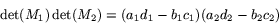 vilket ger att
vilket ger att
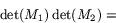
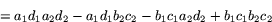
Vidare är
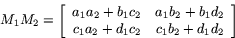
Alltså är
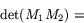
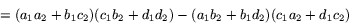
Multiplicerar man nu ihop termerna i det högra ledet ser man att vissa termer tar ut varandra. Det gäller produkterna a1a2c1b2 och b1c2d1d2. Därför förenklas det högra ledet till
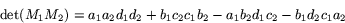
Jämför man nu högra ledet med formeln ovan för 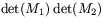 så ser man att de är lika. Detta visar
satsen.
så ser man att de är lika. Detta visar
satsen.
Bevis(av satsen om inversen till en matrisavbildning)
Sätt 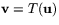 där T är den matrisavbildning vars matris är M. Det innebär att
där T är den matrisavbildning vars matris är M. Det innebär att
v1=au1+bu2, v2=cu1+du2
Låt nu S vara den matrisavbildning vars matris är
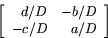 där
där 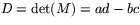 . Då kan man bestämma
. Då kan man bestämma 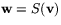 med sambandet
w1=(d/D)v1+(-b/D)v2, w2=(-c/D)v1+(a/D)u2
Sätter vi nu in uttrycken för v1 och v2 så får vi
w1=(d/D)(au1+bu2)+(-b/D)(cu1+du2)=
=((ad-bc)/D)u1 = u1
och
w2=(-c/D)(au1+bu2)+(a/D)(cu1+du2)=
=((ad-bc)/D)u2 = u2
med sambandet
w1=(d/D)v1+(-b/D)v2, w2=(-c/D)v1+(a/D)u2
Sätter vi nu in uttrycken för v1 och v2 så får vi
w1=(d/D)(au1+bu2)+(-b/D)(cu1+du2)=
=((ad-bc)/D)u1 = u1
och
w2=(-c/D)(au1+bu2)+(a/D)(cu1+du2)=
=((ad-bc)/D)u2 = u2
Detta visar att 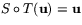 för alla vektorer
för alla vektorer 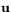 i
i 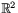 . På liknande sätt ser man att
. På liknande sätt ser man att 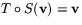 för alla
för alla 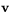 . Det följer att varje vektor
. Det följer att varje vektor 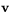 är bild av precis en vektor
är bild av precis en vektor 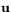 . För det första är
. För det första är 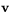 bilden av
bilden av 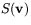 eftersom
eftersom 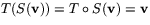 . För det andra kan inte
. För det andra kan inte 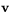 vara bild av två olika
vara bild av två olika 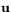 . Om nämligen
. Om nämligen 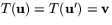 så är
så är 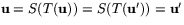 . Detta visar att T är inverterbar och att inversen är S, dvs den avbildning vars matris ges i satsen.
. Detta visar att T är inverterbar och att inversen är S, dvs den avbildning vars matris ges i satsen.
![]() och
och ![]() och antag att
T har matrisen M. Då är
och antag att
T har matrisen M. Då är
![]() och
och ![]() som inte är parallella definierar en parallellogram. I sats 1 kan det emellertid inträffa att
som inte är parallella definierar en parallellogram. I sats 1 kan det emellertid inträffa att ![]() och
och ![]() är parallella. Dessa vektorer definerar då egentligen inte en parallellogram i vanlig mening utan en parallellogram som har kolapsat. Man brukar tala om en urartad parallellogram. En sådan ges arean . Med denna konvention är satsen korrekt oavsett om bilderna av
är parallella. Dessa vektorer definerar då egentligen inte en parallellogram i vanlig mening utan en parallellogram som har kolapsat. Man brukar tala om en urartad parallellogram. En sådan ges arean . Med denna konvention är satsen korrekt oavsett om bilderna av ![]() och
och ![]() är parallella eller inte.
är parallella eller inte.