Inlämningsuppgifter I

1.

En talföljd $a_0,\,a_1,\,a_2,\ldots$ definieras rekursivt av

$$\left\{\begin{array} {l} a_{0}=1/6,\,a_{1}=1/3\ a_{n}=1/6(a_{n-1}+a_{n-2})\mbox{ när }n\geq 2 \end{array}\right.$$

Visa att a_n<1/2ⁿ för alla heltal $n=0,\,1,\,2,\ldots$.

2.

På hur många sätt kan en skolklass med n elever delas in i

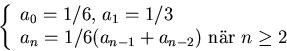
(a)

två icke-tomma grupper betecknade G1 respekitve G2

(b)

två icke-tomma grupper (utan beteckningar)

(c)

tre icke-tomma grupper?

3.

Lös ekvationen

$$z^{6}+{6\choose 1}2z^{5}+{6\choose 2}4z^{4}+{6\choose 3}8z^{3}+{6\choose 4}16z^{2}+{6\choose 5}32z=-65.$$

4.

Lös ekvationen

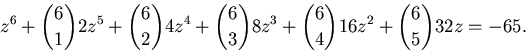
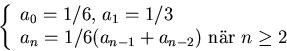
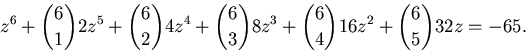
(2-i)z²-(5-5i)z+17-6i=0.

Syftet med inlämningsuppgifterna är dels att Du ska få en chans att kontrollera att Du kan lösa för kursen relevanta uppgifter, dels att Du, genom rättningen, ska få en uppfatting om hur lösningar ska presenteras vid tentamen för att undgå poängavdrag.

Några av uppgifterna är inte så enkla! Sammarbeta gärna! Det viktiga är att Du lyckas förstå och lösa uppgifterna på något sätt och sedan kan skriva ner en självständig lösning. Om Du har ont om tid, koncentrera Dig på några av uppgifterna och lös dem ordentligt. Lösningarna ska lämnas till respektive övningsledare senast fredagen den 2 oktober.