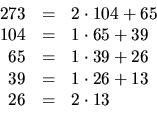
8x-21y=1
med Euklides algoritm för största gemensamma delaren till 21 och 8 baklänges: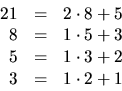
![]()
![]()
![]()
Svar: ![]() där k är ett godtyckligt
heltal. De positiva lösningarna fås när
där k är ett godtyckligt
heltal. De positiva lösningarna fås när ![]() .
.
![]()
![]()
![]()
Svar: 8.
- (a)
- Enligt kinesiska restsatsen finns bara ett tal mindre än
pApBpC(>n) som har resten
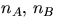 och nC vid
division med
och nC vid
division med 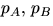 respektive pC. Detta är talet n.
Om man bara känner
t.ex. (nA,pA) och (nB,pB) ger kinesiska restsatsen
att n är något av talen m+kpApB, där m är resten av n
vid division med pApB och k är icke-negativt. Antag att
pA är det minsta av pA och pB.
respektive pC. Detta är talet n.
Om man bara känner
t.ex. (nA,pA) och (nB,pB) ger kinesiska restsatsen
att n är något av talen m+kpApB, där m är resten av n
vid division med pApB och k är icke-negativt. Antag att
pA är det minsta av pA och pB.
Den enda ytterligare information vi har om n är att n<pA3(<pB3) Allt vi vet är att k ska väljas så att m+kpApB<pA3, dvs
Eftersom m<pApB och pA och pB är av samma storleksordning, ger detta ungefär pA möjliga val för k. Eftersom n förutsätts vara stort kommer därför antalet möjligheter för k att vara så stort och det är i praktiken omöjligt att pröva alla möjligheter.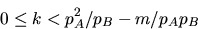
- (b)
- Vi ska lösa ekvationssystemet
Den nedersta ekvationen löses av n=45+101k1, där k1 kan väljas godtyckligt. För att även den andra ekvationen ska lösas krävs att (insättning av n=45+101k1 i den andra ekvationen)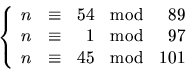
Eftersom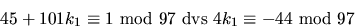
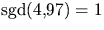 är 4 inverterbart modulo 97 och
multiplikation med en invers till 4 ger
är 4 inverterbart modulo 97 och
multiplikation med en invers till 4 ger
där k2 är ett godtyckligt heltal. De två nedersta ekvationerna stämmer alltså om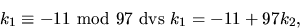
n=45+101k1=45+101(-11+97k2)
Vi bestämmer k2 så att öven den första ekvationen gäller. Insättning av n=45+101(-11+97k2) ger (modulo 89)
Vi ser att vi behöver bestämma en invers till 7 modulo 89. Vi gör detta med Euklides algoritm för största gemensamma delaren till 7 och 89: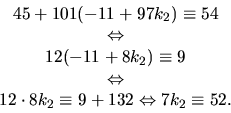
Vi får alltså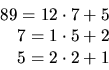
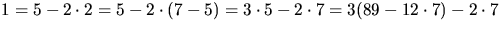 . Modulo 89 ger detta
. Modulo 89 ger detta 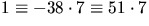 .Detta ger nu
.Detta ger nu
där k3 är godtyckligt. Vi får alltså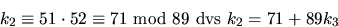
Det minsta icke-negativa talet bland dessa fås när k3=0, dvs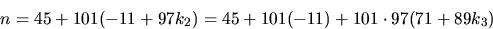
Översättning till bokstäver ger att lösenordet är fideba .
Svar: fideba
![]()
Dett finns bara en delgrupp av ordning 1 och 22. De är ![]() respektive
respektive ![]()
Eftersom 2 och 11 är primtal är (enligt Lagranges
sats) grupper av dessa ordningar cykliska och alltså av formen
![]() för något
för något ![]() .
.
Vi undersöker ![]() och får
och får
![]()
![]()
Svar: Delgrupperna är ![]() samt
samt ![]() .
.