- 4.
- Vi har modulo 32 att
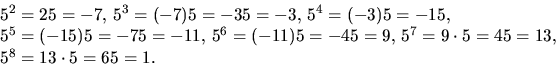
Därmed har 5 ordning 8.
Svar: 8.
- 5.
- Vi bevisar påståendet med induktion.
n=0. När n=0 har vi
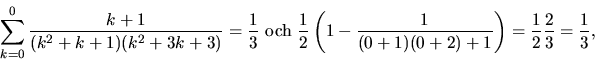
så påståendet gäller då n=0.
Antag nu att påståendet gäller för något värde på n. Vi
visar att då gäller det även för n+1:
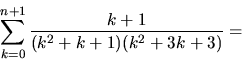
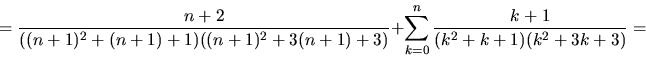
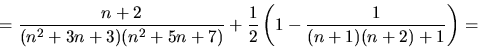
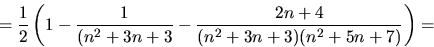
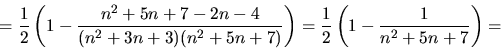
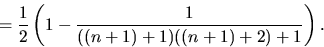
Påståendet gäller alltså även för n+1.
Enligt induktionsprincipen gäller nu påståendet för alla heltal 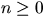 .
.
- 6.
- Det multipla nollstället är ett gemensamt nollställe till
polynomet och dess derivata f'(z)=3z2-(8-6i)z+(2-8i). Vi söker
nollställena till f'(z):
0=f'(z)/3=(z-(4-3i)/3)2-(16-24i-9)/9+(6-24i)/9=(z-(4-3i)/3)2-1/9.
Vi får
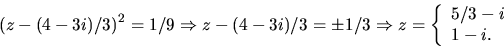
Vi prövar z=1-i i f(z) (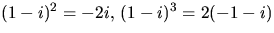 ):
):
f(1+i)=2(-1-i)+(4-3i)2i+(2-8i)(1-i)+2+4i=6+10i+(-6-10i)=0.
Alltså är 1-i ett multipelt nollställe till f(z) och
(z-1+i)2 delar f(z). Vi utför division med (z-1+i)2=
z2-(2-2i)z-2i:
f(z)=(z2-(2-2i)z-2i)(z-(2-i))
Polynomets återstående nollställe är alltså 2-i.
Svar: 1-i med multiplicitet 2 och 2-i.
- 7.
- Antag att Kajsa och Kalle har 9 olika sektioner. De ställer dem
i en rad och sätter in streck i några av de 8 mellanrummen mellan
sektionerna. De som kommer före första strecket (åtminstonde en)
staplas på varandra i tur och ordning. De som hamnar mellan de två
strecken bildar nästa stapel åt höger etc.
Antalet sätt att välja 9 olika sektioner bland 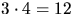 med
hänsyn till ordningen är 12!/3!.
med
hänsyn till ordningen är 12!/3!.
Antalet sätt att välja streck eller inte i de 8 mellanrummen är
28.
Enligt multiplikaitonsprincipen blir svaret
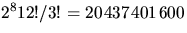 .
.
Svar: 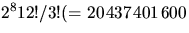 ).
).
- 8.
- Vi skriver uttrycket på gemensamt bråkstreck och får
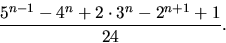
Det gäller alltså att visa att 24 delar täljaren. Eftersom
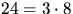 och 3 och 8 är relativt prima räcker det att visa
att 3 och 8 delar täljaren. Vi vill undvika negativa uttryck i
exponenterna och sätter därför m=n-1 och ska visa att
och 3 och 8 är relativt prima räcker det att visa
att 3 och 8 delar täljaren. Vi vill undvika negativa uttryck i
exponenterna och sätter därför m=n-1 och ska visa att
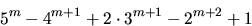
är modulo 3 och 8, när 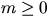 .
.
Räknar vi moldulo 3 blir uttrycket
2m-1m+1-222m+1=2m-2m=0.
Räknar vi modulo 8 får vi
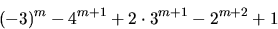
När 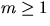 blir detta bara ((-1)m+6)3m+1. Vi har 32=9=1,
så 3m är 1 om m är jämnt och 3 om m är udda:
blir detta bara ((-1)m+6)3m+1. Vi har 32=9=1,
så 3m är 1 om m är jämnt och 3 om m är udda:
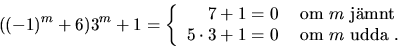
När m=0 blir täljaren 1+4+6-4+1=8=0. Alltså delar även 8
täljaren för alla 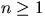 .
.
Därmed är uttrycket ett heltal för alla positiva heltal n.
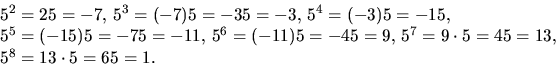
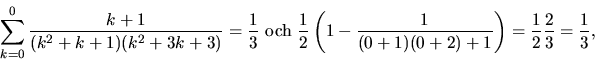
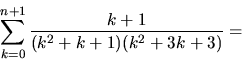
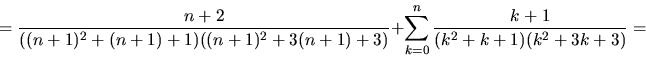
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() med
hänsyn till ordningen är 12!/3!.
med
hänsyn till ordningen är 12!/3!.
![]() .
.![]() ).
).
![]()
![]()
![]()
![]()
![]() .
.