Lösningar till tentamen i MAN011, Aritmetik och algebra, del 1, 98 01 05

3.

(b) Sätt x=3^1/3. Då gäller x³=3, dvs x³-3=0, så 3^1/3 är nollställe till x³-3, vars möjliga rationella nollställen är $\pm 1$ och $\pm 3$. Inget duger, så 3^1/3 är irrationellt.

4.

$$\begin{array} {rcl} 0&=&z^{2}+(-5+3i)z+4-8i=(z+(-5+3i)/2)^{2... ...+3i)/2)^{2}-(25-30i-9)/4+4-8i=(z+(-5+3i)/2)^{2}-i/2.\end{array}$$

Sätt z+(-5+3i)/2=a+bi, där $a,\,b\in \mathbb R,$ och ekvationen blir

i/2=(a+ib)²=a²-b²+2abi.

Detta ger ekvationssystemet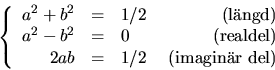

$$\left\{\begin{array} {rclr} a^{2}+b^{2}&=&1/2&\mbox{ (längd... ...realdel)}\ 2ab&=&1/2&\mbox{ (imaginär del)}\end{array}\right.$$

Summan av de två första ekvationerna ger 2a²=1/2, dvs $a=\pm 1/2$. Deras skillnad ger 2b²=1/2, dvs $b=\pm 1/2$. Den tredje ekvationen ger att a och b ska ha samma tecken. Vi får alltså

$$a+bi=\pm (1+i)/2$$

och därmed

$$z+(-5+3i)/2=\pm (1+i)/2\Rightarrow z=(5-3i)/2\pm (1+i)/2\Rightarrow z=\left\{\begin{array} {r} 3-i\ 2-2i\end{array}\right.$$

Svar: $z=3-i,\,2-2i$.

5.

Sätt $x_{1}=x-10,\,y_{1}=y-13,\,z_{1}=z-1$ och ekvationen blir

x₁+y₁+z₁=67.

Uppgiften är den samma som att bestämma antalet till denna ekvation där $x_{1},\,y_{1}z_{1}\geq 0$.

Vi tänker oss 67 ettor i rad och placerar in två streck. Antalet ettor före första strecket är x₁, antalet mellan de två strecken är y₁ och antalet efter det andra är z₁. Antalet lösningar är alltså samma som antalet sätt att placera in två streck på 67+2 platser och sedan placera in ettor på de övriga, dvs

$${69\choose 2}=69\cdot 68/2=69\cdot 34=2346.$$

Svar: 2346.

6.

Sätt t=x², så att x⁶-3x⁴-9x²-5=t³-3t²=9t-5. Möjliga rationella nollställen är $t=\pm 1,\,\pm 5$. När t=5 får vi 125-75-45-5=0. Därmed delar t-5 polynomet enligt Faktorsatsen:

t³-3t²-9t-5=(t-5)(t²+2t+1)=(t-5)(t+1)².

Detta ger

x⁶-3x⁴-9x²-5=(x²-5)(x²+1)².

Möjliga rationella nollställen till x²-5 är $\pm 1,\,\pm 5$. Inget duger så x²-5 är irreducibelt i $\mathbb Q[x],$ medan $x^{2}-5=(x-\sqrt{5})(x+\sqrt{5})$ i $\mathbb R[x]$.

Eftersom $x^{2}+1\geq 1,$ om $x\in \mathbb R,$ är x²+1 irreducibelt i $\mathbb Q[x]$ och $\mathbb R[x],$ medan x²+1=(x-i)(x+i) i $\mathbb C[x]$.

Svar: $\begin{array} {rcl} (x^{2}-5)(x^{2}+1)^{2}&\mbox{ i }& \mathbb Q[x]\ (x-\sq... ...(x-\sqrt{5})(x+\sqrt{5})(x-i)^{2}(x+i)^{2}&\mbox{ i }&\mathbb C[x].\end{array}$

7.

Gruppen $D_{9}=\{r^{i}s^{j}\,\vert\,0\leq i\leq 8,\,0\leq j\leq 1\}$ har ordning 18. Enligt Lagranges sats har en delgrupp en ordning som delar 18.

Eftersom $5\,\not\vert\,18$ saknas delgrupp av ordning 5.

Elementen rⁱs har alla ordning 2 ty

$$r^{i}sr^{i}s=r^{i}r^{-i}ss=1\cdot 1=1.$$

En delgrupp av ordning 9 kan inte innehålla ett element av ordning 2, ty $2\,\not\vert\, 9$. Enda möjliga delgruppen av ordning 9 är därför $C_{9}=\{r^{i}\,\vert\,0\leq i\leq 8\}$.

Av samma skäl kan en delgrupp av ordning 3 inte innehålla något av elementen rⁱs. En sådan delgrupp är alltså en delgrupp till C₉ som är cyklisk och därför har precis en delgrupp av ordning 3 (ty $3\,\vert\,9$).

En delgrupp av ordning 2 är det samma som ett element av ordning 2. Eftersom $2\,\not\vert\, 9$ har C₉ inget element av ordning 2. Delgrupperna av ordning 2 är därför $\{1,\,r^{i}s\},\,0\leq i\leq 8$.

Svar:

9 av ordning 2

1 av ordning 3

av ordning 5

1 av ornding 9.

8.

Antag att a=(5ⁿ-1)/(4ⁿ-1) är ett heltal. Detta ger (4ⁿ-1)a=5ⁿ-1. Räkning modulo 3 ger

$$(0\equiv(1)^{n}-1)a\equiv 2^{n}-1=(-1)^{n}-1\Rightarrow n \mbox{ jämnt.}$$

Räkning modulo 5 ger

$$((-1)^{n}-1)a\equiv -1.$$

Men n ska vara jämnt, så $0\equiv0\cdot a\equiv -1\mbox{ mod }5$. Orimligt.

Svar: (5ⁿ-1)/(4ⁿ-1) är inte ett heltal för något enda positivt heltal.