- (a)
- (b)
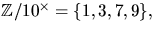 Vi har
Vi har
så gruppen är cyklisk.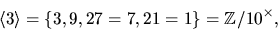
![]()
![]()
![]()
Svar: 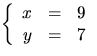 eller
eller 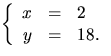
Om z=0, skall x+5y=23. Denna ekvation har 5 lösningar
(motsvarande ![]() eller 4).
eller 4).
Om z=1, skall x+5y=13. Eklvationen har 3 lösningar (![]() eller 2).
eller 2).
Om z=2, skall x+5y=3, som har 1 lösning (y=0).
Alltså finns det totalt 5+3+1=9 sätt att växla 23 kronor.
Svar: 9 sätt.
p(z)=(z-1-i)(z2-3z+1+3i).
Vi vill lösaz2-3z+1+3i=0.
Kvadratkomplettering ger0=z2-3z+1+3i=(z-3/2)2-9/4+1+3i=(z-3/2)2-5/4+3i.
Vi sätter z-3/2=a+bi, där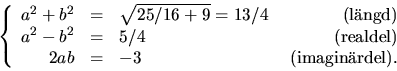
![]()
Svar: 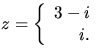
- (a)
- För att visa att
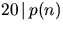 räcker det att visa att
räcker det att visa att 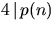 och
och 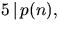 ty
ty 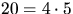 och 4 och 5 är relativt
prima.
och 4 och 5 är relativt
prima.
Modulo 4 gäller
p(n)=n5+2n4+3n3+2n2=n2(n3+2n2+3n+2).
och
så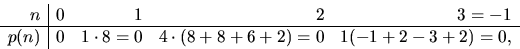
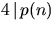 .
.Modulo 5 gäller
Alltså gäller att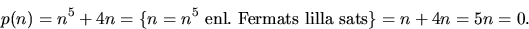
 och därmed att
och därmed att 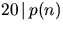 .
. - (b)
- Observera att
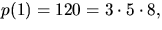 så
så 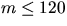 . Vi
undrsöker om
. Vi
undrsöker om 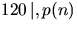 . Det räcker att visa att
. Det räcker att visa att 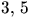 och 8
delar p(n) ty talen är parvis relativt prima och
och 8
delar p(n) ty talen är parvis relativt prima och 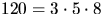 .
.Modulo 3 gäller (n3n enl. Fermats lilla sats)
så 3 delar p(n).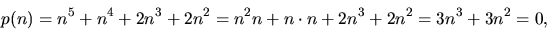
Modulo 8 gäller
p(n)=n5+2n4+3n3+2n2=n2(n3+2n2+3n+2),
och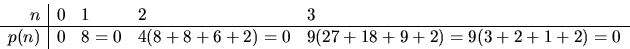
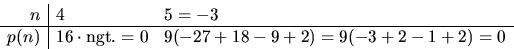
så 8 delar p(n) och därmed gäller att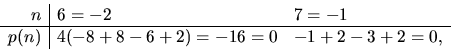
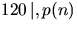 och
m=120.
och
m=120.
Svar: m=120.
Elementen utanför C25 är av formen ![]() och har ordning 2 ty
och har ordning 2 ty ![]() .
.
Elementet ![]() har ordning
har ordning ![]() enligt
satsen om ordningen av ett element i en cyklisk grupp. Vi har alltså
enligt
satsen om ordningen av ett element i en cyklisk grupp. Vi har alltså
![]() och att
o(ri)=25 om i inte delar 25.
och att
o(ri)=25 om i inte delar 25.
Delgrupper av ordning 2. En delgrupp av ordning 2 bestämms av ett element av ordning 2. Det finns 25 sådana:
![]()
Delgrupper av ordning 3. Enligt Lagranges sats delar en
delgrupps ordning gruppens ordning. Eftersom ![]() finns
ingen delgrupp av ordning 3.
finns
ingen delgrupp av ordning 3.
Delgrupper av ordning 5. Eftersom ![]() kan en
delgrupp av ordning 5 inte innehålla ett element av ordning 2. En
delgrupp av ordning 5 är alltså en delgrupp till C5. Enligt
satsen om delgrupper till en cyklisk grupp finns det precis en sådan
av ordning 5 ty
kan en
delgrupp av ordning 5 inte innehålla ett element av ordning 2. En
delgrupp av ordning 5 är alltså en delgrupp till C5. Enligt
satsen om delgrupper till en cyklisk grupp finns det precis en sådan
av ordning 5 ty ![]() .
.
Delgrupper av ordning 10. Låt H vara en delgrupp av
ordning 10. Om ![]() så gäller att
så gäller att
![]() . Detta ger att
. Detta ger att ![]() innehåller något rk där
innehåller något rk där ![]() . Detta ger att
. Detta ger att ![]() är en delgrupp av ordning 5 till C25 (och därmed till
D25). Av detta följer att
är en delgrupp av ordning 5 till C25 (och därmed till
D25). Av detta följer att ![]() (se
ovan). H måste också innehålla något ris och därmed
(se
ovan). H måste också innehålla något ris och därmed
![]() så vi måste ha
så vi måste ha
![]()
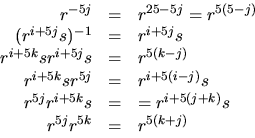
Svar:
| 25 av ordning 2 |
| av ordning 3 |
| 1 av ordning 5 |
| 5 av ordning 10. |