0=z2+(i-4)z+5-5i=(z+(i-4)/2)2-(-1-8i+16)/4+5-5i=(z+(i-4)/2)2+5/4-3i.
Sätter vi z+(i-4)/2=a+bi, där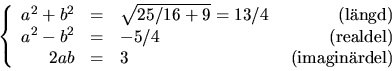
![]()
Svar: ![]() .
.
![]()
![]()
Vi visar nu detta med induktion:
När n=0 har vi a0=1 och 1/(21-1)=1 så formeln stämmer i detta fall.
Antag nu att formeln stämmer för något värde på n. Vi har då
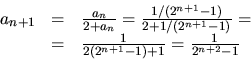
Enligt induktionsprincipen gäller formeln för alla heltal ![]() .
.
Svar: an=1/(2n+1-1).
- (a)
- Vi gör variabelsubstitutionen
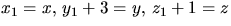 . Ekvationen blir då
. Ekvationen blir då
Denna ekvation har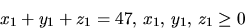
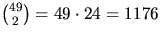 .
.Svar: 1176 stycken heltalslösningar.
- (b)
- Vi bestämmer först antalet lösningat till
Sätter vi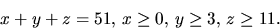
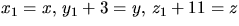 ska vi lösa
ska vi lösa
Denna ekvation har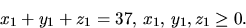
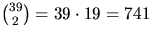 lösningar.
Antalet lösningar till
lösningar.
Antalet lösningar till
Blir därför 1176-741=435.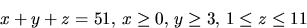
Svar: 435 stycken.
a) Inversen till (1,4,5,3,2) är (1,2,3,5,4) som inte ingår i mängden. Alltså ingen delgrupp.
b) Vi sätter ![]() och
och ![]() så att
mängden är
så att
mängden är ![]() . Följande gäller:
. Följande gäller:
![]()
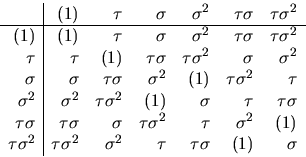
c) Inversen till (1,4,3,5,2) är (1,2,5,3,4) som inte ingår i delmängden. Alltså ingen delgrupp
Svar: Bara mängden i b) är en delgrupp.
![]()
710m+11+611m+10=(72)5m(72)57+611m610= 65m657+611m610.
Vi undersöker potenser av 6 modulo 43 och får![]()
![]()