![]()
n=0. Vi har a0=1 och (1/5)(-2/3)0+1=1+1/5. Alltså gäller påståendet då n=0.
n=1. Vi har a1=2/3 och (1/5)(-2/3)1+1=-2/15+1, så påståendet gäller även när n=1.
Antag nu att an<(1/5)(-2/3)n+1 om n<p, där ![]() .Vi får då
.Vi får då
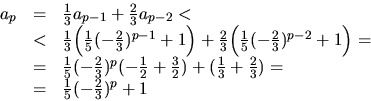
Enligt induktionsprincipen gäller nu påståendet för alla heltal ![]() .
.
0=z2-(5-i)z+8-i=(z-(5-i)/2)2-(25-10i-1)/4+8-i=(z-(5-i)/2)2+2+3i/2.
Vi sätter a+ib=z-(5-i)/2, där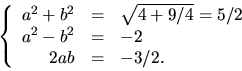
![]()
Svar: ![]()
![]()
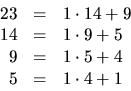
![]()
![]()
Svar: 9257.
![]()
![]()
![]()
![]()
![]()
Svar: ![]() och
och
![]() (av ordning
(av ordning ![]() respektive 10.)
respektive 10.)
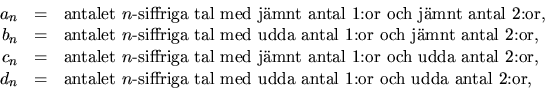
bn=cn,
ty om vi byter 1:or mot 2:or och vice versa ger ett tal av typ b ett av typ c och omvänt.Om vi har ett (n-1)-siffrigt tal av typ c får vi ett n-siffrigt tal av typ c genom att lägga till en 3:a eller en 4:a på slutet. Å andra sidan kan vi få ett n-siffrigt tal av typ c genom att ta ett (n-1)-siffrigt tal av typ a och d genom att lägga till en 2:a respektive en 1:a på slutet. Detta ger
cn=2cn-1+an-1+dn-1
Dett totala antalet (n-1)-siffriga tal är 4n-1 enligt multiplikationsprincipen. Vi har alltså också4n-1=an-1+bn-1+cn-1+dn-1
såan-1+dn-1=4n-1-bn-1-cn-1=4n-1-2cn-1
Detta ger nucn=2cn-1+4n-1-2cn-1=4n-1
Svar: 4n-1.